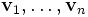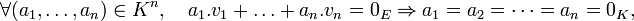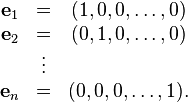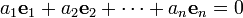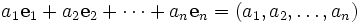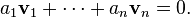Indépendance linéaire - Définition

Introduction

En algèbre linéaire, étant donnée une famille de vecteurs, les vecteurs de la famille sont linéairement indépendants si toute combinaison linéaire finie nulle de ces vecteurs a nécessairement tous ses coefficients nuls. Cela revient à dire qu'aucun des vecteurs de la famille n'est combinaison linéaire finie des autres. Par exemple dans l'espace vectoriel euclidien les trois vecteurs (1,0,0), (0,1,0) et (0,0,1) sont linéairement indépendants, tandis que (2, − 1,1), (1,0,1) et (3, − 1,2) ne sont pas linéairement indépendants. Dans le cas où des vecteurs ne sont pas linéairement indépendants, ils sont dits linéairement dépendants.

Définitions

Soit E un espace vectoriel sur un corps K.

Une famille finie de vecteurs de E est libre, ou encore, la famille est constituée de vecteurs linéairement indépendants si

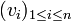
c'est-à-dire, toute combinaison linéaire nulle des vecteurs v_i a nécessairement des coefficients tous nuls (le signe 0 désigne le vecteur nul de E, noté 0_E et l'élément neutre pour l'addition dans K, noté 0_K).

Une famille infinie est libre si toutes ses sous-familles finies le sont : pour toute famille de scalaires tous nuls sauf éventuellement un nombre fini,

.

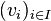
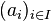
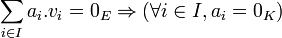
Dans le cas contraire, les vecteurs sont dits linéairement dépendants, ou encore la famille est dite liée. Ainsi, est une famille de vecteurs liée s'il existe une famille d'éléments de K tous nuls sauf un nombre fini, telle que

.

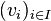
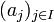
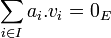
À partir des notions de famille libre ou liée, on définit celles de partie libre ou liée : une partie A de E est dite libre si et seulement si la famille est libre, et elle est dite liée si et seulement si la famille est liée.

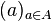
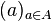
Propriétés

• La famille (v) et la partie {v} sont libres si et seulement si le vecteur v est non nul.
• La famille (v₁,v₂) est liée si et seulement si v₁ et v₂ sont colinéaires (en particulier, la famille (v,v) est toujours liée, que v soit nul ou pas).
• Si l'une des sous-familles d'une famille est liée (en particulier si deux de ses vecteurs sont colinéaires ou si l'un d'entre eux est nul), alors cette famille est liée.
• Inversement, si une famille est libre alors toutes ses sous-familles sont libres.
• Une famille est liée si et seulement si l'un de ses éléments appartient au sous-espace vectoriel engendré par les autres vecteurs de la famille.
• La famille vide et la partie vide sont libres.

Exemples

Exemple 1

Dans l'espace vectoriel R⁴, les trois vecteurs u=(4,2,1,3), v=(2,0,3,0) et w=(6,2,4,-3) sont linéairement indépendants.

Exemple 2

Soit et considérons les éléments suivants de E :

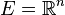
Alors sont linéairement indépendants.

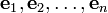
Démonstration

Supposons que a₁, a₂, ..., a_n soient des réels tels que :

Donc

Et ainsi

.

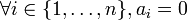
Exemple 3

Les fonctions réelles d'une variable réelle, de classe analytique, forment un sous-espace vectoriel E de l'espace vectoriel réel des fonctions de R dans R. Les fonctions pour λ réel forment une famille infinie non dénombrable de vecteurs linéairement indépendants. La démonstration qui suit montre comment mettre en œuvre le calcul d'un déterminant.

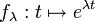
Espace projectif des dépendances linéaires

Une relation de dépendance linéaire de n vecteurs peut être représentée par un n-uplet de n scalaires, non tous nuls, tels que

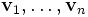
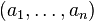
Si une telle relation de dépendance linéaire existe, alors les n vecteurs sont linéairement dépendants. Il est alors possible d'identifier deux relations de dépendances linéaires si l'une est multiple non nul de l'autre relation, parce que dans ce cas les deux correspondent à la même dépendance linéaire des vecteurs entre eux. Sous cette identification, l'ensemble des n-uplets décrivant les dépendances linéaires des vecteurs est un espace projectif.