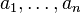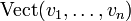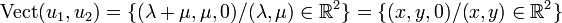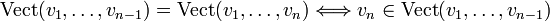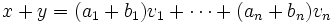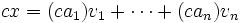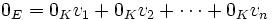Sous-espace vectoriel engendré - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Etant donnée une partie (pas nécessairement finie) A d'un espace vectoriel E sur un corps commutatif K, le sous-espace vectoriel engendré par A est exactement le plus petit sous-espace vectoriel de E contenant A. Des définitions équivalentes sont données ci-dessous. L'engendrement par une famille de vecteurs
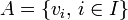
Une famille de vecteurs
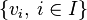
Définitions équivalentes
Soit A une partie (pas nécessairement finie) d'un espace vectoriel E sur un corps commutatif K. Le sous-espace engendré par A peut etre défini comme :
- Le plus petit sous-espace vectoriel de E contenant A, comme dans l'introduction ;
- Ou le sous-ensemble de E des combinaisons linéaires des vecteurs de A.
Ces deux sous-ensembles de E sont égaux : la démonstration doit justifier en particulier que est bien un sous-espace vectoriel de E. Un vecteur appartient à ssi il existe une famille
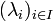
-
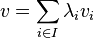
De manière naturelle, est un espace vectoriel. La partie A, contenue dans , est appelée partie génératrice de A, ou ensemble de générateurs de A.
La définition s'étend à une famille quelconque
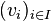
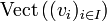
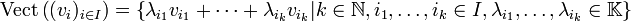
où

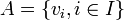
Les familles
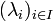
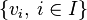
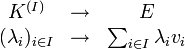
Exemples
- L'espace vectoriel réel
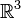
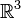
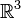
- Dans l'espace vectoriel usuel,
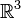
- Soit
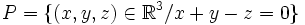
-
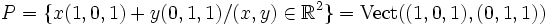
Base
Une base de E est une famille génératrice
Propriétés
- Soient
- La dimension d'un espace vectoriel engendré par une famille de n vecteurs est égale à n si et seulement si la famille est libre.
- Pour toutes parties A et A' de E,
-
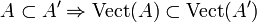
-
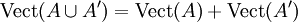
-
Théorèmes
Théorème 1:
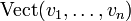
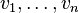
Ce résultat est une des raisons pour lesquelles la notion de sous-espace vectoriel engendré est importante.
Théorème 2: Vect(A) est aussi un sous-espace vectoriel de E. De plus, cet espace vectoriel est le plus petit sous espace-vectoriel de E, contenant A.
Nous n'allons démontrer que le théorème 1. La démonstration du théorème 2 est très similaire, mais un peu plus malaisée à rédiger, puisque les vecteurs de toute combinaison linéaire donnée peuvent être différents.
Démonstration du théorème 1:
Stabilité pour la somme:
Les formes les plus générales possibles pour deux éléments de
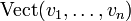
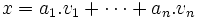
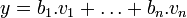
Nous avons à montrer que x + y est aussi une combinaison linéaire de ces vecteurs. En utilisant l'associativité et la commutativité de l'addition ainsi que la distributivité, nous pouvons écrire:
et puisque pour tout i, ai + bi est un scalaire de K, nous voyons que x + y est effectivement une combinaison linéaire des vecteurs donnés.
Stabilité pour la multiplication par un scalaire:
Soit c un scalaire et à nouveau considérons une combinaison linéaire de la forme:
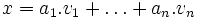
Nous avons à montrer que c.x est aussi une combinaison linéaire de ces vecteurs.
Nous avons
et puisque pour tout i, c.ai est aussi un scalaire le résultat est acquis.
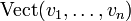
Le vecteur nul de E, 0E est une combinaison linéaire de
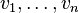
(Ici, 0K est l'élément neutre additif du corps K.)
Cette dernière relation est bien vraie, parce que dans tout espace vectoriel nous avons
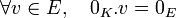
Minimalité:
Supposons que F soit un autre sous-espace vectoriel de E contenant les vecteurs
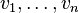
Alors F est stable pour la multiplication et l'addition des vecteurs, ainsi nous pouvons démontrer par une récurrence finie sur le nombre de vecteurs que pour tous scalaires