Liste de critères de divisibilité - Définition

Critère de divisibilité par 32

Un nombre est divisible par 32 si le nombre formé par ses 5 derniers chiffres est divisible par 32.

Exemple

68002175356285458568922152187753216864 est divisible par 32 car 16864 est divisible par 32.

Critère de divisibilité par 31

Lemme de divisibilité par 31

Le nombre est divisible par 31 si et seulement si est divisible par 31.

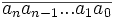
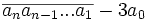
Exemples

1054 est divisible par 31 car

105 – 3 x 4 = 93

et 93 est divisible par 31.

Pour voir si un nombre est divisible par 31 il suffit de répéter l'opération jusqu'à obtenir 0, ce qui montrera que le nombre est divisible par 31.

Soit le nombre 16022567.

On a :

1602256 - 3×7 = 1602235.

160223 - 3×5 = 160208.

16020 - 3×8 = 15996.

1599 - 3×6 = 1581.

158 - 3×1 = 155.

15 - 3×5 = 0.

Nous trouvons 0, donc 16022567 est divisible par 31.

Critère de divisibilité par 34

Un nombre est divisible par 34 s’il est divisible à la fois par 17 et par 2.

Critère de divisibilité par 33

Un nombre est divisible par 33 s’il est divisible à la fois par 11 et par 3.

Critère de divisibilité par 36

Un nombre est divisible par 36 s’il est divisible à la fois par 9 et par 4.

Critère de divisibilité par 35

Un nombre est divisible par 35 s’il est divisible à la fois par 7 et par 5.

Critère de divisibilité par 38

Un nombre est divisible par 38 s’il est divisible à la fois par 19 et par 2.

Critère de divisibilité par 37

Pour savoir si un nombre est divisible par 37, on le sépare par groupe de 3 chiffres à partir des unités en intercalant des +. On effectue l'opération obtenue. Si le résultat est divisible par 37, alors le nombre est divisible par 37.

Exemple

Soit le nombre 19375414619668141953881.

On effectue l'opération :

19 + 375 + 414 + 619 + 668 + 141 + 953 + 881 = 4070

Le résultat ayant plus de 3 chiffres, on peut recommencer une fois

4 + 070 = 74

74 est divisible par 37 donc 19375414619668141953881 est divisible par 37.

Critère de divisibilité par 40

Un nombre est divisible par 40 s’il est divisible à la fois par 8 et par 5.

Critère de divisibilité par 39

Critère immédiat

Un nombre est divisible par 39 s’il est divisible à la fois par 13 et par 3.

Lemme de divisibilité par 39

Le nombre est divisible par 39 si et seulement si est divisible par 39.

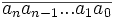
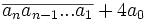
Exemples

702 est divisible par 39 car

70 + 4 x 2 = 78

et 78 est divisible par 39.

Plus généralement, pour voir si un nombre est divisible par 39 il suffit de répéter l'opération jusqu'à obtenir 39, ce qui montrera que le nombre est divisible par 39.

Soit le nombre 49803.

On a :

4980 + 4×3 = 4992.

499 + 4×2 = 507.

50 + 4×7 = 78.

7 + 4×8 = 39.

Nous trouvons 39, donc 49803 est divisible par 39.

Critère de divisibilité par 42

Un nombre est divisible par 42 s’il est divisible à la fois par 7 et par 3 et par 2.

Critère de divisibilité par 41

Lemme de divisibilité par 41

Le nombre est divisible par 41 si et seulement si est divisible par 41.

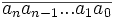
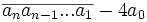
Exemples

1066 est divisible par 41 car

106 – 4 x 6 = 82

et 82 est divisible par 41.

Pour voir si un nombre est divisible par 41 il suffit de répéter l'opération jusqu'à obtenir 0, ce qui montrera que le nombre est divisible par 41.

Considérons le nombre 89011.

On a :

8901 – 4 x 1 = 8897

889 – 4 x 7 = 861

86 – 4 x 1 = 82

8 – 4 x 2 = 0

Nous obtenons 0 donc 89011 est divisible par 41.

Critère pour un grand nombre

Pour savoir si un nombre est divisible par 41, on le sépare par groupe de 5 chiffres à partir des unités en intercalant des +. On effectue l'opération obtenue. Si le résultat est divisible par 41, alors le nombre est divisible par 41

Exemple

Soit le nombre 2136561442277796449261.

On effectue l'opération :

21 + 36561 + 44227 + 77964 + 49261 = 208034

Le résultat ayant plus de 5 chiffres, on peut recommencer une fois

2 + 08034 = 8036

On peut vérifie que 8036 est divisible par 41 en utilisant le lemme de divisibilité par 41.

On a

803 – 4 x 6 = 779

77 – 4 x 9 = 41
4 – 4 x 1 = 0

Nous trouvons 0 donc 2136561442277796449261 est divisible par 41.