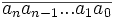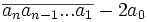Liste de critères de divisibilité - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

Introduction

Ceci est une liste de critères de divisibilité des nombres écrits en base décimale, exposés sans démonstration.

Pour les démonstrations ou les méthodes ayant permis d'établir ces critères, voir l'article Critère de divisibilité.

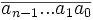
Dans tout cet article, un nombre de n chiffres est représenté par $\overline{a_{n-1}...a_1 a_0}$ .

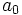
$\qquad a_0$ étant le chiffre des unités.

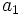
$\qquad a_1$ étant le chiffre des dizaines.

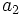
$\qquad a_2$ étant le chiffre des centaines.

Et ainsi de suite.

Entiers inférieurs à 10

Divisibilité par :	Énoncé du critère :	Exemple :
1	Tout nombre entier est divisible par 1	* 1, 2, 3, 4 sont divisibles par 1.
2	Un nombre est pair, c'est-à-dire divisible par 2, si et seulement si son chiffre des unités est 0 ; 2 ; 4 ; 6 ou 8.	* 15679205738 est divisible par 2 car il se termine par 8 qui est un nombre pair ; 450874265809864357898764346892 est divisible par 2 car il se termine par 2.
3	Un nombre est divisible par 3 si et seulement si la somme de ses chiffres est divisible par 3.	35796825 est divisible par 3 car : 3 + 5 + 7 + 9 + 6 + 8 + 2 + 5 = 45 et nous voyons que 45 est divisible par 3. On a même 4 + 5 = 9 (divisible par 3).
4	Un nombre est divisible par 4 si et seulement si le nombre formé par ses deux derniers chiffres est divisible par 4.	* 356812970332548 est divisible par 4 car il se termine par 48 et nous voyons que 48 est divisible par 4.
5	Un nombre est divisible par 5 si et seulement s'il se termine par 0 ou 5.	* 1296837402275 est divisible par 5 car il se termine par 5.
6	* Un nombre est divisible par 6 si et seulement s'il est divisible à la fois par 2 et par 3.	* 24186 est divisible par 6, car : Son chiffre des unités est 6 (chiffre pair) ; Et la somme de ses chiffres vaut 21=3x7.
	* Un nombre est divisible par 6 si et seulement si la somme de son premier chiffre (unité) avec la somme des autres chiffres multipliée 4 donne un multiple de 6.	558 est divisible par 6 car 8+4×(5+5)=48 8+4×4=24 4+2×4=12 2+4×1=6 est un multiple de 6
7	* Le nombre $\overline{a_n a_{n-1}...a_1 a_0}$ est divisible par 7 si et seulement si $\overline{a_n a_{n-1}...a_1 } - 2a_0$ est divisible par 7. Plus simplement un nombre est divisible par 7 si la différence entre le nombre de dizaines et le double du chiffre des unités est divisible par 7.	* 182 est divisible par 7 car : 18 – 2 x 2 = 14 et 14 est divisible par 7. 17381 est divisible par 7 car: 1738 – 2 x 1 = 1736 173 – 2 x 6 = 161 16 – 2 x 1 = 14
	* Il suffit de séparer ce nombre par tranche de 3 chiffres en partant des unités et d'insérer alternativement des - et des + entre les tranches à partir du début du nombre en commençant par un -. On effectue l'opération ainsi écrite et si le résultat est divisible par 7, alors le nombre considéré est divisible par 7. Bien sûr pour voir si le résultat de l'opération précédente est divisible par 7, on peut utiliser le lemme de divisibilité par 7.	*5527579818992. On le sépare par tranche de trois chiffres à partir des unités. 5 \| 527 \| 579 \| 818 \| 992. On intercale alternativement des + et des - à partir du début en commençant par un -. 5 - 527 + 579 - 818 + 992. On effectue l'opération ainsi écrite. 5 - 527 + 579 - 818 + 992 = 231 On regarde si 231 est divisible à l'aide du lemme de divisibilité par 7. 23 - 2×1 = 21 On trouve un résultat divisible par 7 donc 5527579818992 est divisible par 7.
	Méthode de Toja - Découper le nombre par tranches de 2 chiffres et chercher la distance entre chaque nombre de 2 chiffres et le multiple de 7 le plus proche (alternativement par excès et par défaut). Cette méthode ne nécessite pas d'effectuer la division complète mais nécessite de connaître sa table de multiplication par 7 jusqu'à 14.	* 5527579818992. On le sépare par tranches de deux chiffres à partir des unités. 5\|52\|75\|79\|81\|89\|92. A partir de la droite, le multiple de 7 le plus proche par défaut est 91 : distance 92-91=1. Pour la deuxième paire, le multiple de 7 le plus proche par excès est 91 : distance 91-89=2. Pour la troisième paire, le multiple de 7 le plus proche par défaut est 77 : distance 81-77=4 Pour la quatrième paire, distance : 84-79=5 etc... Le nombre de départ est multiple de 7 si et seulement si 1\|2\|4\|5\|5\|4\|5 est multiple de 7 (les différents "restes" sont écrits dans l'ordre inverse) On découpe ce nombre en tranche de 2 chiffres 1\|24\|55\|45 Il est multiple de 7 si et seulement si 3\|1\|3\|6 est multiple de 7 On découpe en tranche de 2 chiffres 31\|36 Qui sera multiple de 7 si et seulement si 1\|4 est multiple de 7 (vrai). Source : (en)divisibilité par 7
8	Un nombre est divisible par 8 si le nombre formé par ses trois derniers chiffres est divisible par 8.	100636136 est divisible par 8 car 136 est divisible par 8.
9	Un nombre est divisible par 9 si la somme de ses chiffres est divisible par 9.	423 est divisible par 9 car 4 + 2 + 3 = 9 et 9 est divisible par 9.
10	Un nombre est divisible par 10 si son chiffre des unités est 0.	1275689573270 est divisible par 10 car il se termine par 0.
$10 n$	Un nombre est divisible par $10 n$ si ses n derniers chiffres sont égaux à 0.	* 154652500000 est divisible par $105$ car ses 5 derniers chiffres sont des 0 ; 2000 est divisible par $103$ car ses trois derniers chiffres sont 0.