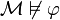Logique intuitionniste - Définition
La liste des auteurs de cet article est disponible ici.
Interprétation de la logique intuitionniste
Approche intuitive
La logique intutionniste peut être vue comme une logique modale, munie de la modalité de nécessité, notée

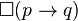
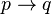
La sémantique de la logique intuitionniste est fondée sur les modèles de Kripke. Ces modèles sont eux-mêmes fondés sur des mondes dans lesquels opèrent la sémantique classique (en 0 et 1 pour le calcul des propositions). Ces mondes peuvent être vus comme des contenus d'information de plus en plus riches. Ils sont donc hiérachisés par une relation d'ordre (la relation d'accessibilité). Si une proposition est « satisfaite » dans un monde, on dit que ce monde force la proposition. Un monde force une proposition
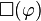

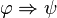

On dira qu'un modèle de Kripke satisfait ou modèlise une proposition si tous les mondes qu'il contient forcent cette proposition.
Une proposition est valide, si elle est satisfaite par tous les modèles.
On peut montrer que la logique intuitionniste est correcte pour les modèles de Kripke, c'est-à-dire que toute proposition prouvable en logique intuitionniste est valide dans les modèles de Kripke.
Or on peut montrer que les propositions suivantes ne sont pas valides pour les modèles de Kripke:
-
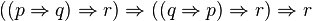
-
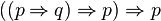
On en conclut que ces deux propositions, qui sont pourtant des tautologies classiques, ne sont pas prouvables en logique intuitionniste.
On montre que les modèles de Kripke sont complets pour la logique intuitionniste, c'est-à-dire que toute proposition valide est prouvable.
Approche formelle
Dans cet article nous ne considèrons que les modèles de la logique propositionnelle qui forment un exemple de sémantique de Kripke.
Un modèle est formé d'un triplet
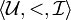
-
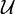
- < est une relation d'ordre ,
Un cône est un ensemble C de mondes (
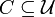
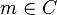
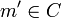
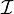
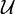
On définit une relation
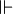

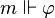

- si φ est une variable x, alors
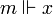
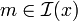
- si φ est une proposition
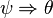
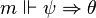
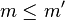
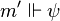
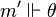
On peut démontrer (par induction sur la structure ou la taille de


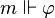
On dit que

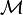
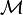

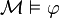
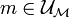
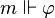

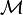
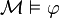
Correction de la logique intuitionniste
On peut montrer que la logique intuitionniste est correcte vis-à-vis des modèles de Kripke, c'est-à-dire que toute proposition démontrable est valide.
Formellement,
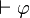
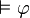
On peut utiliser ce résultat pour montrer qu'une proposition n'est pas démontrable en logique intuitionniste. Si on considère le modèle
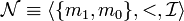
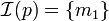
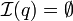
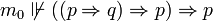
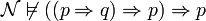
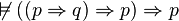
On peut aussi trouver un contre-modèle très simple de la proposition
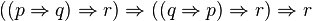
Complétude de la logique intuitionniste
On peut démontrer que toute proposition valide est démontrable.
Formellement,
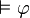
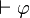
La démonstration se fait de la façon suivante: si