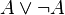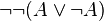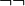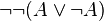Logique intuitionniste - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Approche informelle - Interprétation de la logique intuitionniste - Approche formelle - Bibliographie - Relations avec la logique classique

Bibliographie

Dirk van Dalen, Logic and structure, Springer-Verlag, 1991.
Jean-Yves Girard, Le point aveugle, Tome I, Hermann, 2007.
Jean Largeault, L'Intuitionisme, Paris, Presses universitaires de France, 1992.
Jean Largeault, Intuitionisme et théorie de la démonstration, Paris, Vrin, 1992.

Relations avec la logique classique

Inclusion de la logique classique dans la logique intuitionniste

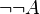
Si l’on admet la démonstration faite par Kurt Gödel, que l’insertion de double-négations placées selon des règles définies, nommée « Non-non traduction de Gödel-Kolmogorov » (voir ci-après), permet de rendre démontrable en logique intuitionniste toute formule démontrable en logique classique ; et si l’on considère qu’en logique intuitionniste, $\lnot \lnot A$ est une forme affaiblie de $A$ , alors il est possible d’assimiler la logique classique à une forme affaiblie de la logique intuitionniste et de voir la logique classique comme inclue dans la logique intuitionniste. Remarque : si l’on admet cela, on peut également faire remarquer que la logique intuitionniste n’est pas « moins capable » que la logique classique (voir les exposés qui suivent).

De manière plus économe que la saturation des formules et sous-formules par des doubles négations Gödel a remarqué que si on considère une fonction f : de l'ensemble des formules dans l'ensemble des formules définie par :

f (faux) = faux
f (X) = non ( non (X) ), pour une formule atomique X différente du faux
f ( A et B) = f (A) et f(B)
f (A ou B) = non [ non( f (A) ) et non( f (B) ) ]
f (A → B) = f(A) → f(B)
f ( all x P(x) ) = all x f ( P(x) )
f ( exists x P(x) ) = non ( all x non f ( P(x) )

Où A et B sont des formules quelconques et P est une formule ayant x comme paramètre.

alors on a le théorème suivant :

Gamma |-c A ⇔ f (Gamma) |-i f (A).

Où "|-c" est la déduction classique et "|-i" est la déduction intuitionniste.

La Non-non traduction

Ce qui amena Brouwer à concevoir l’intuitionnisme étant une remise en cause de la qualité des preuves de la logique classique, une question peut venir : quelle est donc la valeur d’une preuve de la logique classique du point de vue de la logique intuitionniste ? Dans le cas de la preuve de l’hypothèse qu’il existe des a et b irrationnels tels que a^b soit rationnel (voir plus haut), la preuve de cette affirmation par le tiers-exclus est-elle fausse ? Il serait contradictoire de l’affirmer, puisque le théorème de Gelfond-Schneider indique que effectivement, l’une des deux hypothèses utilisées est concrètement vraie, et qu’il existe des solutions qui permettent d’en donner des exemples à l’œuvre. Cependant, comme vu précédemment, elle apporte une réponse… incomplète (elle ne réalise pas de solution). On pourra dire assez honnêtement, que la preuve par le tiers-exclus, montre au moins que l’affirmation de l’hypothèse qu’elle « démontre », n’est pas une contradiction. 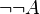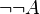La preuve de la non-contradiction d’une hypothèse $A$ selon la logique intuitionniste étant la preuve de $\lnot \lnot A$ , c’est finalement la preuve de $\lnot \lnot A$ (qui signifie que $A$ peut éventuellement être démontré) qu’a effectuée la démonstration par la logique classique. Cette constatation est le fondement de la Non-non traduction, qui permet d’exprimer une formule de la logique classique en logique intuitionniste (voir ). Ce principe a été formalisé par Kurt Gödel et Andreï Kolmogorov.

Attention : la Non-non traduction est une traduction dans un seul sens. Bien qu’elle permette de traduire une expression de la logique classique en termes de la logique intuitionniste, elle ne garantit par l’inverse (mais l’inverse reste possible dans certains cas, comme il peut l’être trivialement pour une formule traduite de la logique classique). 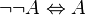De plus et ne serait-ce que pour la raison que, par exemple en logique classique $\lnot \lnot A \Leftrightarrow A$ ou encore qu’en logique classique les opérateurs peuvent être exprimés les uns par rapport aux autres, la Non-non traduction ne peut pas être bijective : plusieurs expressions de la logique classique peuvent correspondre à une même expression de la logique intuitionniste.

La question des preuves non-constructives

Bien que le principe de la logique intuitionniste soit la preuve constructive, nous avons vu qu’il est possible de traduire une expression de la logique classique en logique intuitionniste. Cela amène à ce poser la question des expressions de la logique intuitionniste, qui correspondraient à des expressions de la logique classique (suite à une traduction ou non). 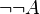Nous avons vu que ces expressions peuvent faire usage de $\lnot \lnot A$ qui signifie que $A$ n’est pas contradictoire. Les preuves faites sur de telles expressions ne traiteront pas de choses concrètes, mais de potentialités (contradictoire ou non-contradictoire) ; ce qui n’amène pas à exposer une solution au sens propre du terme, puisque l’objet, est la proposition. La logique intuitionniste, peut donc également faire des démonstrations non-constructives ; mais ces démonstrations sont alors identifiées comme telles, et ne dise rien de plus que « cela est contradictoire » ou « cela n’est pas contradictoire ». La logique intuitionniste peut donc produire des preuves ayant sens pour la logique classique. Une interprétation de cette remarque, est que la logique intuitionniste, éclaire ce que fais la logique classique, en donnant une interprétation de ce que sont les preuves classiques.

La question du tiers-exclus

La négation $\lnot$ n’ayant pas le même sens en logique intuitionniste qu’en logique classique, explique que $A \lor \lnot A$ ne soit pas toujours valide en logique intuitionniste (après tout, des similitudes syntaxiques n’indiquent pas nécessairement des similitudes sémantiques). Cependant, il existe une formulation du tiers-exclus de la logique classique, qui est (en termes intuitionniste) $\lnot \lnot (A \lor \lnot A)$ . Cette expression reste toujours valide, même si $A$ n’est pas décidable (c’est une conséquence de la signification du $\lnot \lnot$ , qui a été présenté plus haut). Cette interprétation, « même si $A$ n’est pas décidable $\lnot \lnot (A \lor \lnot A)$ est toujours démontrable », est une autre mise en lumière la raison pour laquelle le tiers-exclus classique ne peut pas fonder une preuve intuitionniste : son interprétabilité est faible.