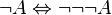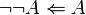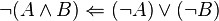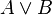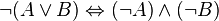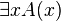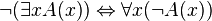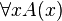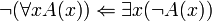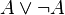Logique intuitionniste - Définition
La liste des auteurs de cet article est disponible ici.
Approche formelle
Nous venons de voir que l'implication et la disjonction ne sont plus liées. Mais en fait cela va plus loin : une des caractéristiques de la logique intuitionniste est le fait que chaque connecteur
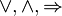

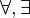
La logique implicative minimale
Pour introduire la logique intuitionniste, le plus simple est de commencer par la déduction naturelle en logique implicative minimale, qui est la logique propositionnelle dans laquelle il n'y a qu'un connecteur, l'implication
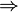
En déduction naturelle,
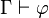
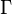

Il y a alors deux règles (voir plus bas Lecture des règles) :

La première règle s'appelle la règle d'élimination de l'implication, tandis que la seconde règle s'appelle la règle d'introduction de l'implication. On remarque que l'élimination de l'implication est aussi le modus ponens bien connu. La méthode qui consiste à avoir pour chaque connecteur une (ou des) règle(s) d'élimination et une (ou des) règle(s) d'introduction est typique de la déduction naturelle et nous allons la retrouver par la suite.
Ce système de déduction est très simple (rasoir d'Ockham), mais il est moins puissant que la logique classique, car on ne peut y démontrer ni la loi de Peirce
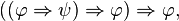
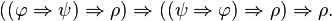
Lecture des règles
La règle d'élimination de l'implication peut se lire comme suit : si de l'ensemble d'hypothèses Γ je déduis
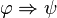


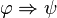
La logique propositionnelle intuitionniste
On conserve les règles de la logique implicative minimale concernant l'implication.
L'absurde
L'absurde est la proposition, notée

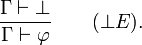
Cela signifie que si un ensemble de propositions Γ conduit à l'absurde, alors de cet ensemble de propositions Γ, je peux déduire n'importe quelle proposition

Cette règle est aussi la règle d'élimination de l'absurde. Il n'y a pas (heureusement!) de règle d'introduction de l'absurde. Le nom de cette règle ne doit pas la faire confondre avec la règle de raisonnement par l'absurde (reductio ad absurdum) qui n'existe pas en logique intuitionniste. En effet le raisonnement par l'absurde est étroitement lié au tiers exclu et n'est pas constructif.
Remarque: en logique classique cette règle n'est pas utile, car elle est une conséquence du raisonnement par l'absurde.
La négation
Traditionnellement, on considère la négation comme une abréviation. Plus précisément on dit que
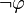
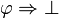
La conjonction
On introduit un nouveau connecteur binaire
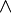
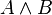
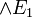
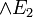

La disjonction
On introduit un nouveau connecteur binaire
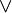
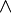
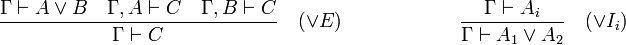
On remarque que la règle d'élimination de la disjonction est une règle tryadique, c'est-à-dire qu'elle a trois prémisses.
Le calcul des prédicats intuitionniste
Le calcul des prédicats intuitionniste reprend toutes les règles du calcul propositionnel intuitionniste ci-dessus et lui adjoint de nouvelles règles pour les quantificateurs "quel que soit" et "il existe". Son langage et son ensemble de formules demeurent les mêmes que ceux du calcul des prédicats classique
Remarque : Nous rappelons que A[t/x] signifie le remplacement de toutes les occurrences librement substituables de la variable x par le terme t ; voir calcul des prédicats pour les notions de "variable", "terme", "substitution" et de "librement substituable".
Le quantificateur universel
- Règle d'introduction :
- Gamma |- A
- ----------------------
- Gamma |- All x A
- Règle d'élimination :
- Gamma, A[t/x] |- B
- ------------------------------
- Gamma, All x A |- B
Le quantificateur existentiel
- Règle d'introduction :
- Gamma |- A[t/x]
- ---------------------------
- Gamma |- Exists x A
- Règle d'élimination :
- Gamma, A |- B
- -------------------------------
- Gamma, Exists x A |- B
Exemples de différences avec la logique classique
Les opérations ne sont pas définies l’une par rapport à l’autre (voir plus loin), et ne sont définies qu’en elles-mêmes. Elles sont définies par l’interprétation qui soit en être faites. Pour cette raison, en plus des règles de calcul, sont données les interprétations qui doivent être faites des expressions de chaque opérateurs.
Negation
- Interprétation : « Il est démontré que A est contradictoire » (et non pas « A est Faux »).
- Attention : il ne faut pas en conclure que
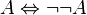
Double-négation
- Interprétation : « Il est prouvé qu’il est contradictoire d’affirmer que A est contradictoire », c’est à dire « Il est prouvé que A n’est pas contradictoire » (et en particulier, surtout pas « A est Vrai »).
- C’est à dire
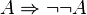
- Attention : la réciproque n’est pas vraie, on a pas
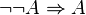
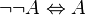
- L’expression
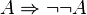
- Remarque : la non-contradiction de A, bien qu’insuffisante pour constituer une preuve de A, reste tout de même une condition nécessaire à cette démonstration.
Conjonction
- Interprétation : « Preuve que A et preuve que B » (comparable à ce qu’il en est en logique classique).
- C’est à dire
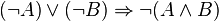
- Contrairement à ce qu’il en serait en logique classique,
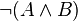
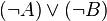
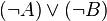
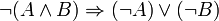
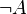
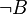
Disjonction
- Interprétation : « Preuve que A ou preuve que B » (et en particulier, surtout pas « Preuve que A ou B »).
- A et B s’excluent mutuellement et ne sont pas simultanément vrai.
- Comparable à ce qu’il en serait dans la logique classique de Bool et Carnaug.
Quantificateur existentiel
- Interprétation : « Nous savons comment créer un x et pouvons prouvez que A(x) » (et non pas « Il existe théoriquement un x vérifiant A(x) »)
- S’il n’existe pas de x qui vérifie A(x) alors pour tous les x on ne vérifie pas A(x), d’où l’équivalence (qui correspond à l’intuition et se formule naturellement).
- Comparable à ce qu’il en serait en logique classique.
Quantificateur universel
- Interprétation : « Preuve que pour chaque x appartenant à l’ensemble spécifié, nous pouvons toujours prouver A(x) » (comparable à ce qu’il en est en logique classique).
- C’est à dire
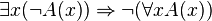
- Contrairement à ce qu’il en serait en logique classique,
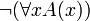
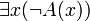
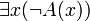
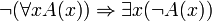
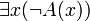
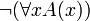
Tiers-exclus
- Cette relation qui n’est pas a priori valide, peut cependant être valide ! Elle n’est seulement pas automatiquement valide, et elle n’en est pas plus automatiquement invalide. Elle est valide si nous pouvons prouver A ou prouver
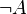
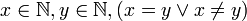
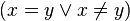
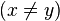
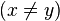
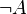
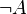
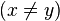
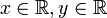
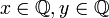
Relations entre les règles
Pour mieux comprendre, on remarquera dans ce qui précède, que contrairement à ce qu’il en est dans la logique de Bool, la conjonction
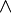
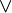
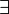

Concernant la disjonction
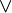

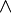
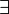
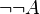
Les interprétations des expressions ne se font pas dans le sens de Vrai et Faux, mais dans le sens de Prouvable et Contradictoire. C’est ce qui explique que nous ne disposons pas de tables de calcul, comme avec l’algèbre de Boole, ce qui ensuite, explique pourquoi les opérations ne puissent pas être redéfinis dans les termes d’une autre.