Dimanche 27 Avril 2025
Rechercher 🔍

Loi du zéro-un de Borel - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Énoncé - Limite supérieure d'ensembles

Introduction

La loi du zéro-un de Borel a été publiée en 1909 dans l'article Les probabilités dénombrables et leurs applications arithmétiques, par Émile Borel, en vue, semble-t-il, d'applications aux propriétés des fractions continues. Un peu plus tard, Cantelli aurait remarqué et utilisé le fait que, pour l'un des deux sens, l'hypothèse d'indépendance est superflue, ce qui conduit au lemme de Borel-Cantelli, d'un usage courant en probabilités : un exemple phare est sûrement la démonstration, par Kolmogorov, de la loi forte des grands nombres.

Énoncé

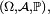
Dans un espace probabilisé \scriptstyle\ \left(\Omega, \mathcal A, \mathbb{P}\right), considérons une suite \scriptstyle\ (A_n)_{n\ge 0} d'éléments de \scriptstyle\ \mathcal{A} (ou "évènements"). La loi du zéro-un de Borel stipule que :

Loi du zéro-un de Borel — Si les événements \scriptstyle\ A_n sont indépendants, alors
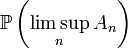
\mathbb{P}\left(\limsup_n A_n\right)
vaut 0 ou 1 suivant que la série de terme général \scriptstyle\ \mathbb{P}(A_n) est convergente ou divergente.
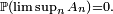
  • Si la série de terme général \scriptstyle\ \mathbb{P}(A_n) est convergente, alors, en vertu du lemme de Borel-Cantelli, on a \scriptstyle\ \mathbb{P}\left(\limsup_n A_n\right)=0. C'est dans ce sens que l'hypothèse d'indépendance est superflue.
  • Supposons que la série de terme général \scriptstyle\ \mathbb{P}(A_n) est divergente, et montrons que
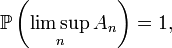
\mathbb{P}\left(\limsup_n A_n\right)=1,

ou, de manière équivalente, montrons que

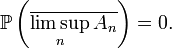
\mathbb{P}\left(\overline{\limsup_n A_n}\right)=0.

On rappelle que

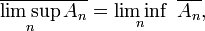
\overline{\limsup_n A_n} = \liminf_n\ \overline{A_n},

d'après les lois de De Morgan. Plus précisément,

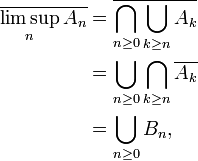
\begin{align} \overline{\limsup_n A_n} &= \overline{\bigcap_{n\ge0}\bigcup_{k\ge n} A_k} \\ &= \bigcup_{n\ge0}\bigcap_{k\ge n}\overline{A_k} \\ &= \bigcup_{n\ge0}B_n, \end{align}

où

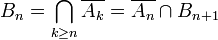
B_n= \bigcap_{k\ge n}\overline{A_k} =\overline{A_n}\cap B_{n+1}

est une suite croissante d'évènements. Ainsi

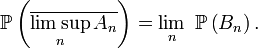
\mathbb{P}\left(\overline{\limsup_n A_n}\right)=\lim_n\ \mathbb{P}\left(B_n\right).

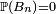
On conclut en montrant que \scriptstyle\ \mathbb{P}\left(B_n\right)=0 . Posons

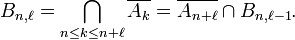
B_{n,\ell}= \bigcap_{n\le k\le n+\ell}\overline{A_k} =\overline{A_{n+\ell}}\cap B_{n,\ell-1}.

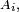
En vertu de l'indépendance des \scriptstyle\ A_i,

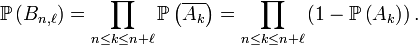
\mathbb{P}\left(B_{n,\ell}\right)= \prod_{n\le k\le n+\ell}\mathbb{P}\left(\overline{A_k}\right) =\prod_{n\le k\le n+\ell}\left(1-\mathbb{P}\left(A_k\right)\right).

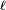
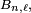
En vertu de la décroissance en \scriptstyle\ \ell de \scriptstyle\ B_{n,\ell},

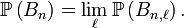
\mathbb{P}\left(B_{n}\right)= \lim_{\ell} \mathbb{P}\left(B_{n,\ell}\right).

Or on a :

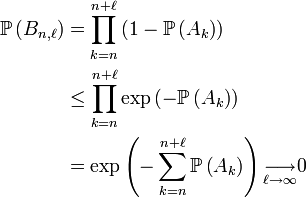
\begin{align} \mathbb{P}\left(B_{n,\ell}\right) &= \prod_{k=n}^{n+\ell} \left(1-\mathbb{P}\left(A_k\right)\right) \\ &\le \prod_{k=n}^{n+\ell}\exp\left(-\mathbb{P}\left(A_k\right)\right) \\ &= \exp\left(-\sum_{k=n}^{n+\ell}\mathbb{P}\left(A_k\right)\right) \underset{\ell \rightarrow \infty}{\longrightarrow}0 \end{align}

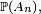
par convexité de l'exponentielle puis divergence de la série de terme général \scriptstyle\ \mathbb{P}\left(A_n\right),\ ce qui achève la démonstration.

Limite supérieure d'ensembles

Définition —  La limite supérieure \scriptstyle \limsup_n\, A_n d'une suite \scriptstyle\ (A_n)_{n\ge 0}\, de parties d'un ensemble \scriptstyle \Omega est l'ensemble des éléments \scriptstyle \omega de \scriptstyle \Omega tels que l'assertion \scriptstyle \{\omega\in A_k\} soit vérifiée pour une infinité d'indices \scriptstyle k\ge 0 .

En d'autres termes, on peut dire que \scriptstyle\ \omega\in\limsup_n\, A_n si et seulement si l'ensemble \scriptstyle \{k\ge 0\ \vert\ \omega\in A_k\} est infini, ou bien non borné. Une formulation équivalente est la suivante : pour tout \scriptstyle n\ge 0 , on peut trouver \scriptstyle k\ge n tel que \scriptstyle \omega\in A_k . Cette dernière formulation fournit une écriture commode de la limite supérieure d'ensembles à l'aide d'opérations élémentaires sur les ensembles :

\limsup_n A_n =\bigcap_{n\ge 0}(\bigcup_{k\ge n} A_k).

Sous l'influence de la terminologie anglo-saxonne, on dira aussi parfois que \scriptstyle\ \omega\in\limsup_n\, A_n si et seulement si \scriptstyle\ \{\omega\in A_k\}\ "infiniment souvent" ou bien "infinitely often", d'où la notation rencontrée dans certains ouvrages :

\mathbb{P}\left(\limsup_n A_n\right)=\mathbb{P}\left(A_n\quad\text{i.o.}\right).

La définition " \scriptstyle\ \omega\in\limsup_n\, A_n si et seulement si \scriptstyle\ \omega\ appartient à une infinité de \scriptstyle\ A_k\ " peut induire en erreur : si, par exemple, toutes les parties \scriptstyle\ A_k\ sont égales, il se peut que \scriptstyle\ \omega\ appartienne à \scriptstyle\ A_k\ pour une infinité d'indices \scriptstyle\ k\ , et il se peut donc que \scriptstyle\ \omega\ appartienne à \scriptstyle\ \limsup_n\, A_n, sans pour autant qu' \scriptstyle\ \omega\ appartienne à une infinité de \scriptstyle\ A_k\ (puisqu'il n'existe, au fond, qu'un seul \scriptstyle\ A_k ).

- Introduction - Énoncé - Limite supérieure d'ensembles
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
Page générée en 0.106 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise