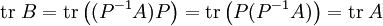Matrices semblables - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, deux matrices carrées A et B sont dites semblables s'il existe une matrice inversible P telle que :
- A = PBP − 1.
Il s'agit d'une relation d'équivalence.
Deux matrices sont semblables si et seulement si elles constituent deux matrices représentatives du même endomorphisme dans deux bases (éventuellement) différentes. Il ne faut pas confondre la notion de matrices semblables avec celle de matrices équivalentes. En revanche, si deux matrices sont semblables, alors elles sont équivalentes. Un moyen de déterminer si deux matrices sont semblables est de les réduire, c'est-à-dire de les ramener à une forme type : diagonale, forme réduite de Jordan…
Exemple
Les matrices suivantes sont semblables :
-
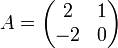
-
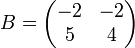
En effet, en posant :
-
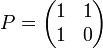
on obtient :
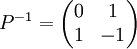
et on vérifie aisément que :
-
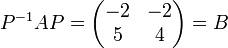
Invariants de similitude
Les applications de l'espace des matrices carrées dont le résultat est identique pour une matrice et une matrice qui lui est semblable sont appelés invariants de similitude. En particulier, la trace d'une matrice est un invariant de similitude. Avec les notations précédentes :
De même, le rang, le déterminant, les valeurs propres, le polynôme caractéristique et le polynôme minimal sont des invariants de similitudes, mais ils ne suffisent pas toujours à détecter la non-similitude de deux matrices. Un système complet d'invariants est décrit dans l'article Invariants de similitude.