Méthode de Sotta - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe de la méthode - Application à la résolution des équations de degré 4 - Application à la résolution des équations de degré 3 - Application à la résolution des équations de degré 6 - Application à la résolution des équations de degré 5 - Cas général - Application à la résolution des équations de degré 7 - Équations dont l'équation résolvante admet une racine nulle - Compléments - Exemples - Équations dont l'équation résolvante admet une racine double - Méthodes trigonométriques de Sotta - Méthode paramétrique de Sotta - Méthode trigonométrique de Sotta en tangente kpi/7 - Méthode trigonométrique de Sotta en tangente kpi/9 - Méthode trigonométrique de Sotta en cosinus kpi/7 - Méthode trigonométrique de Sotta en cosinus kpi/9 - Autres méthodes de résolution d'équations

Méthode trigonométrique de Sotta en tangente kpi/7

Soit à résoudre l'équation :

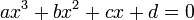
$a x^3 + b x^2 + c x + d = 0 ~$

On choisit h et k tel que $\frac{h}{k}$ soit racine de l'une des deux équations suivantes (résolvantes trigonométriques en pi/7) :

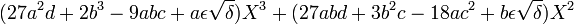
$(27a^2d + 2b^3 - 9abc + a\epsilon \sqrt{\delta})X^3 + (27abd + 3b^2c - 18ac^2 + b\epsilon \sqrt{\delta})X^2 ~$

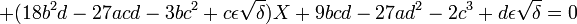
$+ (18b^2d - 27acd - 3bc^2 + c \epsilon \sqrt{\delta})X + 9bcd - 27ad^2 - 2c^3 + d \epsilon \sqrt{\delta} = 0 ~$

$ε$ prenant successivement les valeurs $ε$ = 1 et $ε$ = -1.

On retiendra la valeur de $ε$ qui fournit une résolvante trigonométrique ayant une racine la plus simple possible (le plus souvent une racine évidente). si aucune des deux valeurs de $ε$ ne permet d'avoir une racine s'exprimant simplement, on peut considérer que la méthode a échoué.

On choisit ensuite p et q tel que :

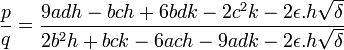
$\frac{p}{q} = \frac{9adh - bch + 6bdk - 2c^2k - 2\epsilon.h\sqrt{\delta}}{2b^2h + bck - 6ach - 9adk - 2\epsilon.h\sqrt{\delta}} ~$

On pose ensuite :

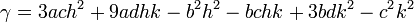
$\gamma = 3ach^2 + 9adhk - b^2h^2 - bchk + 3bdk^2 - c^2k^2 ~$

Les racines de l'équation à résoudre sont alors :

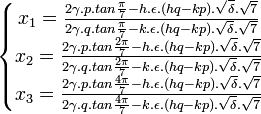
$\left\{\begin{matrix} x_1 = \frac{2\gamma .p. tan \frac{\pi}{7} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}{2\gamma .q. tan \frac{\pi}{7} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}} \\ x_2 = \frac{2\gamma .p. tan \frac{2\pi}{7} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}{2\gamma .q. tan \frac{2\pi}{7} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}} \\ x_3 = \frac{2\gamma .p. tan \frac{4\pi}{7} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}{2\gamma .q. tan \frac{4\pi}{7} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}} \end{matrix}\right. ~$

La méthode que l'on vient de voir permet de trouver les racines d'un polynôme du troisième degré en fonction de $t a n (k π / 7)$ .Sans utiliser une autre méthode, on peut exprimer les racines trouvée en fonction de $s i n (k π / 7)$ ou $c o s (k π / 7)$ . Il suffit, pour cela, d'utiliser les formules de conversion suivantes :

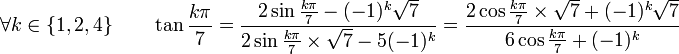
$\forall k \in \{1, 2, 4 \} \qquad \tan \frac{k\pi}{7} = \frac{2\sin \frac{k\pi}{7} - (-1)^k \sqrt{7}}{2\sin \frac{k\pi}{7} \times \sqrt{7} - 5(-1)^k } = \frac{2\cos \frac{k\pi}{7}\times \sqrt{7} + (-1)^k \sqrt{7}}{6\cos \frac{k\pi}{7} + (-1)^k } ~$

Exemple 7

Soit à résoudre l'équation :

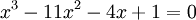
$x^3 - 11x^2 - 4x + 1 = 0 ~$

On a :

$a = 1 \qquad b = -11 \qquad c = -4 \qquad d = 1 ~$

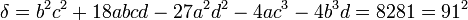
$\delta = b^2c^2 + 18abcd - 27a^2d^2 - 4ac^3 - 4b^3d = 8281 = 91^2 ~$

Des deux résolvantes trigonométriques, seule celle correspondant à $ε$ = 1, a des racines évidentes.

Cette résolvante trigonométrique est :

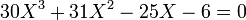
$30X^3 + 31X^2 - 25X - 6 = 0 ~$

Dont l'une des racines est:

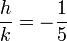
$\frac{h}{k} = -\frac{1}{5} ~$

On peut donc choisir h = -1 et k = 5.

Ensuite :

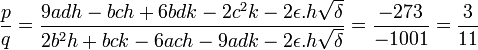
$\frac{p}{q} = \frac{9adh - bch + 6bdk - 2c^2k - 2\epsilon.h\sqrt{\delta}}{2b^2h + bck - 6ach - 9adk - 2\epsilon.h\sqrt{\delta}} = \frac{-273}{-1001} = \frac{3}{11} ~$

On peut choisir p = 3 et q = 11.

Ensuite :

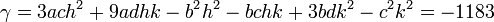
$\gamma = 3ach^2 + 9adhk - b^2h^2 - bchk + 3bdk^2 - c^2k^2 = -1183 ~$

Les racines de l'équation à résoudre sont alors :

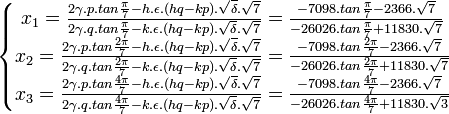
$\left\{\begin{matrix} x_1 = \frac{2\gamma .p. tan \frac{\pi}{7} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}{2\gamma .q. tan \frac{\pi}{7} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}} = \frac{-7098.tan\frac{\pi}{7} - 2366.\sqrt{7}}{-26026.tan \frac{\pi}{7} + 11830.\sqrt{7}}\\ x_2 = \frac{2\gamma .p. tan \frac{2\pi}{7} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}{2\gamma .q. tan \frac{2\pi}{7} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}} = \frac{-7098.tan\frac{2\pi}{7} - 2366.\sqrt{7}}{-26026.tan \frac{2\pi}{7} + 11830.\sqrt{7}} \\ x_3 = \frac{2\gamma .p. tan \frac{4\pi}{7} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}{2\gamma .q. tan \frac{4\pi}{7} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{7}}= \frac{-7098.tan\frac{4\pi}{7} - 2366.\sqrt{7}}{-26026.tan \frac{4\pi}{7} + 11830.\sqrt{3}} \end{matrix}\right. ~$

Qui se simplifie sous la forme :

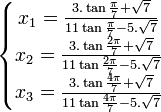
$\left\{\begin{matrix} x_1 = \frac{3.\tan\frac{\pi}{7} + \sqrt{7}}{11\tan \frac{\pi}{7} - 5.\sqrt{7}} \\ x_2 = \frac{3.\tan\frac{2\pi}{7} + \sqrt{7}}{11\tan \frac{2\pi}{7} - 5.\sqrt{7}} \\ x_3 = \frac{3.\tan\frac{4\pi}{7} + \sqrt{7}}{11\tan \frac{4\pi}{7} - 5.\sqrt{7}} \end{matrix}\right. ~$

En utilisant les formules de conversion :

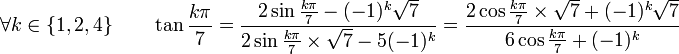
les racines de l'équation proposée peuvent s'écrire :

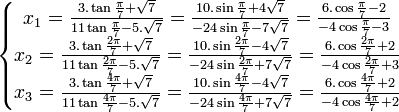
$\left\{\begin{matrix} x_1 = \frac{3.\tan\frac{\pi}{7} + \sqrt{7}}{11\tan \frac{\pi}{7} - 5.\sqrt{7}} = \frac{10.\sin\frac{\pi}{7} + 4\sqrt{7}}{-24\sin \frac{\pi}{7} - 7\sqrt{7}} = \frac{6.\cos\frac{\pi}{7} - 2}{-4\cos \frac{\pi}{7} - 3}\\ x_2 = \frac{3.\tan\frac{2\pi}{7} + \sqrt{7}}{11\tan \frac{2\pi}{7} - 5.\sqrt{7}}= \frac{10.\sin\frac{2\pi}{7} - 4\sqrt{7}}{-24\sin \frac{2\pi}{7} + 7\sqrt{7}} = \frac{6.\cos\frac{2\pi}{7} + 2}{-4\cos \frac{2\pi}{7} + 3} \\ x_3 = \frac{3.\tan\frac{4\pi}{7} + \sqrt{7}}{11\tan \frac{4\pi}{7} - 5.\sqrt{7}}= \frac{10.\sin\frac{4\pi}{7} - 4\sqrt{7}}{-24\sin \frac{4\pi}{7} + 7\sqrt{7}} = \frac{6.\cos\frac{4\pi}{7} + 2}{-4\cos \frac{4\pi}{7} + 2} \end{matrix}\right. ~$

Méthode trigonométrique de Sotta en tangente kpi/9

Soit à résoudre l'équation :

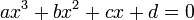
$a x^3 + b x^2 + c x + d = 0 ~$

On choisit h et k tel que $\frac{h}{k}$ soit racine de l'une des deux équations suivantes (résolvantes trigonométriques en pi/9) :

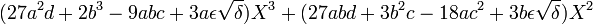
$(27a^2d + 2b^3 - 9abc + 3a\epsilon \sqrt{\delta})X^3 + (27abd + 3b^2c - 18ac^2 + 3b\epsilon \sqrt{\delta})X^2 ~$

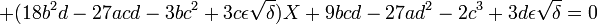
$+ (18b^2d - 27acd - 3bc^2 + 3c \epsilon \sqrt{\delta})X + 9bcd - 27ad^2 - 2c^3 + 3d \epsilon \sqrt{\delta} = 0 ~$

$ε$ prenant successivement les valeurs $ε$ = 1 et $ε$ = -1.

On choisit ensuite p et q tel que :

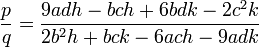
$\frac{p}{q} = \frac{9adh - bch + 6bdk - 2c^2k}{2b^2h + bck - 6ach - 9adk} ~$

On pose ensuite :

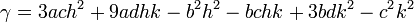
$\gamma = 3ach^2 + 9adhk - b^2h^2 - bchk + 3bdk^2 - c^2k^2 ~$

Les racines de l'équation à résoudre sont alors :

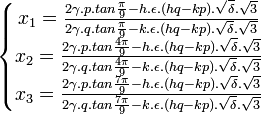
$\left\{\begin{matrix} x_1 = \frac{2\gamma .p. tan \frac{\pi}{9} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}}{2\gamma .q. tan \frac{\pi}{9} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}} \\ x_2 = \frac{2\gamma .p. tan \frac{4\pi}{9} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}}{2\gamma .q. tan \frac{4\pi}{9} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}} \\ x_3 = \frac{2\gamma .p. tan \frac{7\pi}{9} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}}{2\gamma .q. tan \frac{7\pi}{9} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}} \end{matrix}\right. ~$

La méthode que l'on vient de voir permet de trouver les racines d'un polynôme du troisième degré en fonction de $t a n (k π / 9)$ .Sans utiliser une autre méthode, on peut exprimer les racines trouvées en fonction de $s i n (k π / 9)$ ou $c o s (k π / 9)$ . Il suffit, pour cela, d'utiliser les formules de conversion suivantes :

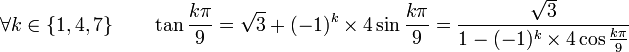
$\forall k \in \{1, 4, 7 \} \qquad \tan \frac{k\pi}{9} = \sqrt{3} + (-1)^k \times 4\sin \frac{k\pi}{9} = \frac{\sqrt{3}}{1 - (-1)^k \times 4\cos \frac{k\pi}{9}} ~$

Exemple 6

Soit à résoudre l'équation :

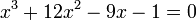
$x^3 + 12x^2 - 9x - 1 = 0 ~$

On a :

$a = 1 \qquad b = 12 \qquad c = -9 \qquad d = -1 ~$

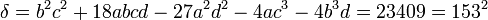
$\delta = b^2c^2 + 18abcd - 27a^2d^2 - 4ac^3 - 4b^3d = 23409 = 153^2 ~$

Des deux résolvantes trigonométriques, seule celle correspondant à $ε$ = 1, a des racines évidentes.

Cette résolvante trigonométrique est :

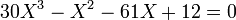
$30X^3 - X^2 - 61X + 12 = 0 ~$

Dont l'une des racines est:

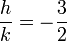
$\frac{h}{k} = -\frac{3}{2} ~$

On peut donc choisir h = 3 et k = -2.

Ensuite :

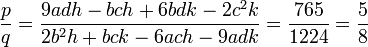
$\frac{p}{q} = \frac{9adh - bch + 6bdk - 2c^2k}{2b^2h + bck - 6ach - 9adk} = \frac{765}{1224} = \frac{5}{8} ~$

On peut choisir p = 5 et q = 8.

Ensuite :

$\gamma = 3ach^2 + 9adhk - b^2h^2 - bchk + 3bdk^2 - c^2k^2 = -2601 ~$

Les racines seront :

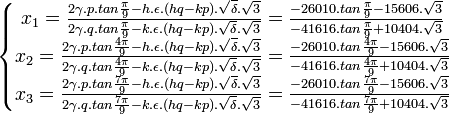
$\left\{\begin{matrix} x_1 = \frac{2\gamma .p. tan \frac{\pi}{9} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}}{2\gamma .q. tan \frac{\pi}{9} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}} = \frac{-26010.tan\frac{\pi}{9} - 15606.\sqrt{3}}{-41616.tan \frac{\pi}{9} + 10404.\sqrt{3}} \\ x_2 = \frac{2\gamma .p. tan \frac{4\pi}{9} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}}{2\gamma .q. tan \frac{4\pi}{9} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}} = \frac{-26010.tan\frac{4\pi}{9} - 15606.\sqrt{3}}{-41616.tan \frac{4\pi}{9} + 10404.\sqrt{3}} \\ x_3 = \frac{2\gamma .p. tan \frac{7\pi}{9} - h. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}}{2\gamma .q. tan \frac{7\pi}{9} - k. \epsilon .(hq - kp). \sqrt{\delta}. \sqrt{3}} = \frac{-26010.tan\frac{7\pi}{9} - 15606.\sqrt{3}}{-41616.tan \frac{7\pi}{9} + 10404.\sqrt{3}} \end{matrix}\right. ~$

Qui se simplifie sous la forme :

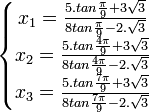
$\left\{\begin{matrix} x_1 = \frac{5.tan\frac{\pi}{9} + 3\sqrt{3}}{8tan \frac{\pi}{9} - 2.\sqrt{3}} \\ x_2 = \frac{5.tan\frac{4\pi}{9} + 3\sqrt{3}}{8tan \frac{4\pi}{9} - 2.\sqrt{3}} \\ x_3 = \frac{5.tan\frac{7\pi}{9} + 3\sqrt{3}}{8tan \frac{7\pi}{9} - 2.\sqrt{3}} \end{matrix}\right. ~$

En utilisant les formules de conversion :

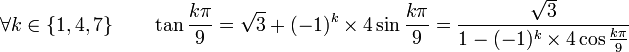
$\forall k \in \{1, 4, 7 \} \qquad \tan \frac{k\pi}{9} = \sqrt{3} + (-1)^k \times 4\sin \frac{k\pi}{9} = \frac{\sqrt{3}}{1 - (-1)^k \times 4\cos \frac{k\pi}{9}} ~$

les racines de l'équation proposée peuvent s'écrire :

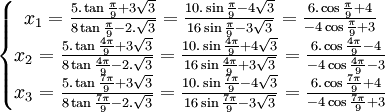
$\left\{\begin{matrix} x_1 = \frac{5.\tan\frac{\pi}{9} + 3\sqrt{3}}{8\tan \frac{\pi}{9} - 2.\sqrt{3}} = \frac{10.\sin\frac{\pi}{9} - 4\sqrt{3}}{16\sin \frac{\pi}{9} - 3\sqrt{3}} = \frac{6.\cos\frac{\pi}{9} + 4}{-4\cos \frac{\pi}{9} + 3}\\ x_2 = \frac{5.\tan\frac{4\pi}{9} + 3\sqrt{3}}{8\tan \frac{4\pi}{9} - 2.\sqrt{3}}= \frac{10.\sin\frac{4\pi}{9} + 4\sqrt{3}}{16\sin \frac{4\pi}{9} + 3\sqrt{3}} = \frac{6.\cos\frac{4\pi}{9} - 4}{-4\cos \frac{4\pi}{9} - 3} \\ x_3 = \frac{5.\tan\frac{7\pi}{9} + 3\sqrt{3}}{8\tan \frac{7\pi}{9} - 2.\sqrt{3}}= \frac{10.\sin\frac{7\pi}{9} - 4\sqrt{3}}{16\sin \frac{7\pi}{9} - 3\sqrt{3}} = \frac{6.\cos\frac{7\pi}{9} + 4}{-4\cos \frac{7\pi}{9} + 3} \end{matrix}\right. ~$

Remarque

Dans l'exemple 6, la résolvante trigonométrique avait d'autres racines évidentes que -3/2. Nous avions aussi la racine évidente :

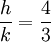
$\frac{h}{k} = \frac{4}{3} ~$

Nous aurions pu alors choisir :

$h = 4 \qquad k = 3 ~$

Nous aurions alors abouti aux racines :

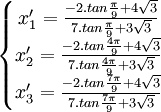
$\left\{\begin{matrix} x_1' = \frac{-2.tan\frac{\pi}{9} + 4\sqrt{3}}{7.tan \frac{\pi}{9} + 3\sqrt{3}} \\ x_2' = \frac{-2.tan\frac{4\pi}{9} + 4\sqrt{3}}{7.tan \frac{4\pi}{9} + 3\sqrt{3}} \\ x_3' = \frac{-2.tan\frac{7\pi}{9} + 4\sqrt{3}}{7.tan \frac{7\pi}{9} + 3\sqrt{3}} \end{matrix}\right. ~$

Qui contrairement aux apparences sont bien les mêmes racines que précédemment. Nous avons en effet :

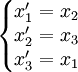
$\left\{\begin{matrix} x_1' = x_2 \\ x_2' = x_3 \\ x_3' = x_1 \end{matrix}\right. ~$

Ces identifications nous permettent d'en déduire les formules:

$\left\{\begin{matrix} \tan \frac{4\pi}{9}. \tan\frac{\pi}{9} = \frac{\tan \frac{4\pi}{9} - \tan\frac{\pi}{9}}{\sqrt{3}} - 1 \\ \tan \frac{7\pi}{9}. \tan\frac{4\pi}{9} = \frac{\tan \frac{7\pi}{9} - \tan\frac{4\pi}{9}}{\sqrt{3}} - 1 \\ \tan \frac{\pi}{9}. \tan\frac{7\pi}{9} = \frac{\tan \frac{\pi}{9} - \tan\frac{7\pi}{9}}{\sqrt{3}} - 1 \end{matrix}\right. ~$

Méthode paramétrique de Sotta

Méthode trigonométrique de Sotta en cosinus kpi/7

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Page générée en 0.126 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise