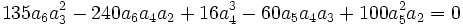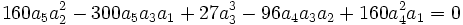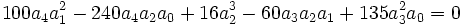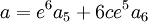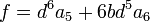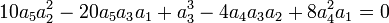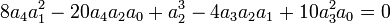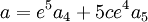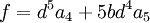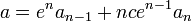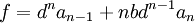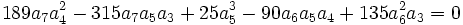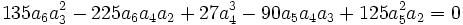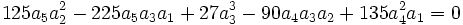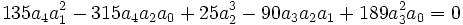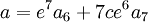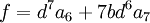Méthode de Sotta - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe de la méthode - Application à la résolution des équations de degré 4 - Application à la résolution des équations de degré 3 - Application à la résolution des équations de degré 6 - Application à la résolution des équations de degré 5 - Cas général - Application à la résolution des équations de degré 7 - Équations dont l'équation résolvante admet une racine nulle - Compléments - Exemples - Équations dont l'équation résolvante admet une racine double - Méthodes trigonométriques de Sotta - Méthode paramétrique de Sotta - Méthode trigonométrique de Sotta en tangente kpi/7 - Méthode trigonométrique de Sotta en tangente kpi/9 - Méthode trigonométrique de Sotta en cosinus kpi/7 - Méthode trigonométrique de Sotta en cosinus kpi/9 - Autres méthodes de résolution d'équations

Application à la résolution des équations de degré 6

Les équations de degré 6 :

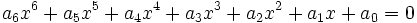
$\qquad a_6 x^6 + a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0$

admettent des racines sous la forme :

$\qquad \frac{b\sqrt[6]{a} - c\sqrt[6]{f}}{d\sqrt[6]{a} - e\sqrt[6]{f}}$

seulement si :

$\qquad 135a_6a_3^2-240a_6a_4a_2+16a_4^3-60a_5a_4a_3+100a_5^2a_2=0$
$\qquad 160a_5a_2^2-300a_5a_3a_1+27a_3^3-96a_4a_3a_2+160a_4^2a_1=0$
$\qquad 100a_4a_1^2-240a_4a_2a_0+16a_2^3-60a_3a_2a_1+135a_3^2a_0=0$

Par conséquent, la méthode de Sotta ne permet de résoudre que les équations de degré 6 vérifiant ces conditions de résolubilité.

Soit donc l'équation suivante :

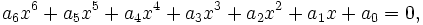
$\qquad a_6 x^6 + a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0,$

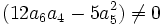
Premier cas : Si $(12a_6a_4-5a_5^2) \not = 0$ (condition pour que la résolvante soit du second degré).

La résolvante de Sotta associée sera :

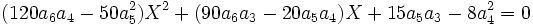
$\qquad (120a_6a_4-50a_5^2)X^2 + (90a_6a_3-20a_5a_4)X + 15a_5a_3 - 8a_4^2= 0$

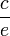
Il suffit donc de choisir b, c, d, e tel que $\frac{b}{d}$ et $\frac{c}{e}$ soit les racines de la résolvante. On calcule ensuite a et f à l'aide des formules :

$a = e^6a_5+6ce^5a_6 ~$
$f = d^6a_5+6bd^5a_6 ~$

Les six racines de l'équation à résoudre seront :

$\qquad x_k = \frac{be^{\frac{2ki\pi}{6}}\sqrt[6]{a} - c\sqrt[6]{f}}{de^{\frac{2ki\pi}{6}}\sqrt[6]{a} - e\sqrt[6]{f}}$ avec k prenant successivement les valeurs 0, 1, 2, 3, 4, 5.

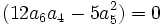
Deuxième cas : Si $(12a_6a_4-5a_5^2) = 0$ .

Voir le paragraphe en fin d'article.

Application à la résolution des équations de degré 5

Les équations de degré 5 :

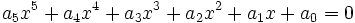
$\qquad a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0$

admettent des racines sous la forme :

$\qquad \frac{b\sqrt[5]{a} - c\sqrt[5]{f}}{d\sqrt[5]{a} - e\sqrt[5]{f}}$

seulement si :

$\qquad 10a_5a_2^2-20a_5a_3a_1+a_3^3-4a_4a_3a_2+8a_4^2a_1=0$
$\qquad 8a_4a_1^2-20a_4a_2a_0+a_2^3-4a_3a_2a_1+10a_3^2a_0=0$

Par conséquent, la méthode de Sotta ne permet de résoudre que les équations de degré 5 vérifiant ces conditions de résolubilité.

Soit donc l'équation suivante :

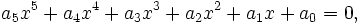
$\qquad a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0,$

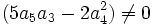
Premier cas : Si $(5a_5a_3-2a_4^2) \not = 0$ (condition pour que la résolvante soit du second degré).

La résolvante de Sotta associée sera :

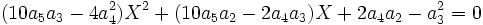
$\qquad (10a_5a_3-4a_4^2)X^2 + (10a_5a_2-2a_4a_3)X + 2a_4a_2 - a_3^2= 0$

Il suffit donc de choisir b, c, d, e tel que $\frac{b}{d}$ et $\frac{c}{e}$ soit les racines de la résolvante. On calcule ensuite a et f à l'aide des formules :

$a = e^5a_4+5ce^4a_5 ~$
$f = d^5a_4+5bd^4a_5 ~$

Les cinq racines de l'équation à résoudre seront :

$\qquad x_k = \frac{be^{\frac{2ki\pi}{5}}\sqrt[5]{a} - c\sqrt[5]{f}}{de^{\frac{2ki\pi}{5}}\sqrt[5]{a} - e\sqrt[5]{f}}$ avec k prenant successivement les valeurs 0, 1, 2, 3, 4.

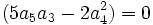
Deuxième cas : Si $(5a_5a_3-2a_4^2) = 0$ .

Voir le paragraphe en fin d'article.

Cas général

Les équations de degré n supérieur ou égal à 4:

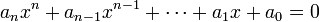
$\qquad a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0 = 0 ~$

admettent des racines sous la forme :

$\qquad \frac{b\sqrt[n]{a} - c\sqrt[n]{f}}{d\sqrt[n]{a} - e\sqrt[n]{f}}$

seulement si :

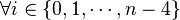
$\forall i \in \{0,1, \cdots ,n-4\} ~$

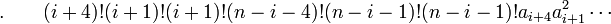
$.\qquad (i+4)!(i+1)!(i+1)!(n-i-4)!(n-i-1)!(n-i-1)!a_{i+4}a_{i+1}^2 \cdots ~$

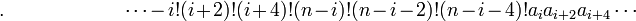
$.\qquad \qquad \qquad \cdots - i!(i+2)!(i+4)!(n-i)!(n-i-2)!(n-i-4)!a_ia_{i+2}a_{i+4} \cdots ~$

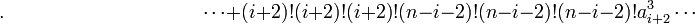
$.\qquad \qquad \qquad \qquad \qquad \cdots + (i+2)!(i+2)!(i+2)!(n-i-2)!(n-i-2)!(n-i-2)!a_{i+2}^3 \cdots ~$

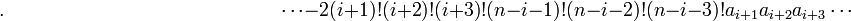
$.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \cdots - 2(i+1)!(i+2)!(i+3)!(n-i-1)!(n-i-2)!(n-i-3)!a_{i+1}a_{i+2}a_{i+3} \cdots ~$

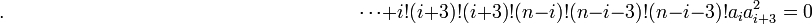
$.\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \cdots + i!(i+3)!(i+3)!(n-i)!(n-i-3)!(n-i-3)!a_ia_{i+3}^2 = 0 ~$

Par conséquent, la méthode de Sotta ne permet de résoudre que les équations de degré n vérifiant cette condition de résolubilité.

Soit donc l'équation suivante :

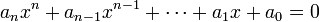
$\qquad a_n x^n + a_{n - 1} x^{n - 1} + \cdots + a_1 x + a_0 = 0 ~$

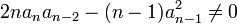
Premier cas : Si $2na_na_{n-2}-(n-1)a_{n-1}^2 \neq 0 ~$ (condition pour que la résolvante soit du second degré).

La résolvante de Sotta associée sera :

$\qquad (n-1)(n-2)[2na_na_{n-2}-(n-1)a_{n-1}^2]X^2 + 2(n-1)[3na_na_{n-3}-(n-2)a_{n-1}a_{n-2}]X + 6(n-1)a_{n-1}a_{n-3} - 4(n-2)a_{n-2}^2= 0$

Il suffit donc de choisir b, c, d, e tel que $\frac{b}{d}$ et $\frac{c}{e}$ soit les racines de la résolvante. On calcule ensuite a et f à l'aide des formules :

$\qquad a = e^na_{n-1}+nce^{n-1}a_n$
$\qquad f = d^na_{n-1}+nbd^{n-1}a_n$

Les n racines de l'équation à résoudre seront :

$\qquad x_k = \frac{be^{\frac{2ki\pi}{n}}\sqrt[n]{a} - c\sqrt[n]{f}}{de^{\frac{2ki\pi}{n}}\sqrt[n]{a} - e\sqrt[n]{f}}$ avec k prenant successivement toutes les valeurs entières de 0 à n-1

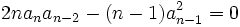
Deuxième cas : Si $2na_na_{n-2}-(n-1)a_{n-1}^2 = 0 ~$ .

Voir le paragraphe ci-après.

Application à la résolution des équations de degré 7

Les équations de degré 7 :

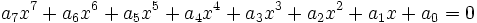
$\qquad a_7 x^7 + a_6 x^6 + a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0$

admettent des racines sous la forme :

$\qquad \frac{b\sqrt[7]{a} - c\sqrt[7]{f}}{d\sqrt[7]{a} - e\sqrt[7]{f}}$

seulement si :

$\qquad 189a_7a_4^2-315a_7a_5a_3+25a_5^3-90a_6a_5a_4+135a_6^2a_3=0$
$\qquad 135a_6a_3^2-225a_6a_4a_2+27a_4^3-90a_5a_4a_3+125a_5^2a_2=0$
$\qquad 125a_5a_2^2-225a_5a_3a_1+27a_3^3-90a_4a_3a_2+135a_4^2a_1=0$
$\qquad 135a_4a_1^2-315a_4a_2a_0+25a_2^3-90a_3a_2a_1+189a_3^2a_0=0$

Par conséquent, la méthode de Sotta ne permet de résoudre que les équations de degré 7 vérifiant ces conditions de résolubilité.

Soit donc l'équation suivante :

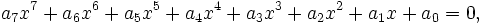
$\qquad a_7 x^7 + a_6 x^6 + a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x + a_0 = 0,$

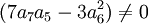
Premier cas : Si $(7a_7a_5-3a_6^2) \neq 0$ (condition pour que la résolvante soit du second degré).

La résolvante de Sotta associée sera :

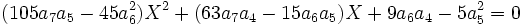
$\qquad (105a_7a_5-45a_6^2)X^2 + (63a_7a_4-15a_6a_5)X + 9a_6a_4 - 5a_5^2= 0$

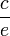
Il suffit donc de choisir b, c, d, e tel que $\frac{b}{d}$ et $\frac{c}{e}$ soit les racines de la résolvante. On calcule ensuite a et f à l'aide des formules :

$a = e^7a_6+7ce^6a_7 ~$
$f = d^7a_6+7bd^6a_7 ~$

Les sept racines de l'équation à résoudre seront :

$\qquad x_k = \frac{be^{\frac{2ki\pi}{7}}\sqrt[7]{a} - c\sqrt[7]{f}}{de^{\frac{2ki\pi}{7}}\sqrt[7]{a} - e\sqrt[7]{f}}$ avec k prenant successivement les valeurs 0, 1, 2, 3, 4, 5, 6.

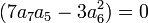
Deuxième cas : Si $(7a_7a_5-3a_6^2) = 0$ .

Voir le paragraphe en fin d'article.

Équations dont l'équation résolvante admet une racine nulle

Nous avons stipulé en début d'article que l'équation à résoudre devait vérifier la condition :

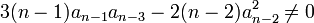
$3(n-1)a_{n-1}a_{n-3} - 2(n-2)a_{n-2}^2 \neq 0 ~$

Si cette condition n'est pas vérifiée alors que le coefficient de degrés deux n'est pas nul, l'équation résolvante admet une racine nulle et dans ce cas la méthode ne peut pas, en général, aboutir.

Il y a toutefois une exception si l'équation à résoudre vérifie de plus la condition :

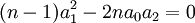
$(n-1)a_1^2 - 2na_0a_2 = 0 ~$

Dans ce cas, on peut appliquer la méthode normalement.

Application à la résolution des équations de degré 3

Compléments

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

Page générée en 0.127 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise