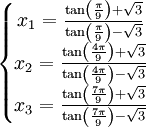Méthode de Sotta - Définition
La liste des auteurs de cet article est disponible ici.
Équations dont l'équation résolvante admet une racine double
Soit
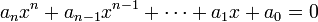
Une équation à résoudre satisfaisant les conditions de résolubilité et dont l'équation résolvante admet une racine double α.
α est alors racine multiple d'ordre n-1 de l'équation à résoudre et la racine simple β manquante est obtenue par la relation :
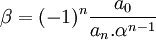
Plus précisément, l'équation à résoudre peut alors s'écrire :
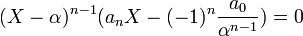
Remarque : Les racines α et β ne sont pas égales sinon tous les coefficients de l'équation résolvante seraient nul.
Méthodes trigonométriques de Sotta
L'ambition des méthodes trigonométriques n'est pas de résoudre toutes les équations du troisième degré, mais de détecter et de calculer dans celles-ci des racines sous l'une des formes suivantes :
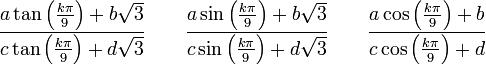
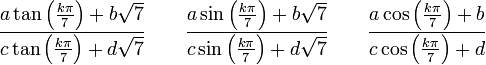
a, b, c, d étant le plus souvent des entiers relatifs.
Plutôt que d'appliquer le procédé utilisé dans l'exemple 5 pour chaque équation que l'on doit résoudre, ce qui est assez fastidieux, il est plus judicieux de l'appliquer à l'équation générale du troisième degré :
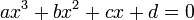
et de retenir le résultat sous forme de méthode.
Dans tout ce qui suit on pose :
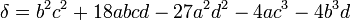
δ est le discriminant de l'équation et sera un carré parfait si l'équation a des racines sous l'une des formes recherchées.
À chacune des formes recherchées corresponds une méthode trigonométrique permettant d'exprimer directement les solutions sous cette forme.
Nous allons exposer ci-dessous quelques-unes de ces méthodes en donnant des formules de conversion pour convertir les solutions trouvées d'une forme à une autre.
Toutes les méthodes trigonométriques peuvent être retrouvées à l'aide de la méthode paramétrique exposée plus haut.
Méthode paramétrique de Sotta
Soit à résoudre l'équation :
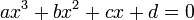
La méthode paramétrique consiste à faire un changement de variable en posant :
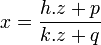
On obtient alors une nouvelle équation du troisième degré en z dont les coefficients dépendent des paramètres h, p, k, q. On se propose alors de déterminer les paramètres de façon à obtenir par exemple :
- soit une simplification par les racines cubiques comme dans l'exemple 3.
- soit une apparition de fonctions trigonométriques comme dans l'exemple 4.
- etc.
Plutôt que d'exposer en détail la méthode qui est très fastidieuse, nous l'illustrerons par l'exemple suivant :
Exemple 5
Soit à résoudre l'équation :
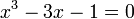
Nous allons appliquer ici la méthode paramétrique dans le but d'améliorer le procédé utilisé dans l'exemple 4. Les calculs qui suivent étant assez fastidieux, il est conseillé d'utiliser une calculatrice travaillant en calcul formel ou un logiciel capable de manipuler les expressions littérales.
Posons :
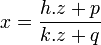
avec :
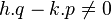
En portant ce changement de variable dans l'équation à résoudre, on trouve une nouvelle équation du troisième degré, d'inconnue z, dont les coefficients dépendent des paramètres h,p,k,q : :
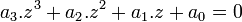
avec :
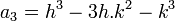
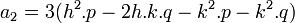
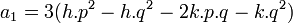
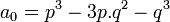
Les paramètres h,p,k,q seront déterminées ultérieurement de façon à ce qu'apparaissent des fonctions trigonométriques comme dans l'exemple 4.
La résolvante de Sotta se factorise sous la forme :
![-9(h.q - k.p)^2.[(h^2 + h.k + k^2)Z^2 + (2h.p + h.q + k.p + 2k.q)Z + p^2 + p.q + q^2] = 0 ~](https://static.techno-science.net/illustration/Definitions/autres/4/409707e048c87516f08477373fa7ab10_dadf8f604a45114cf71c18aae8fad77e.png)
Quel que soit l'équation de départ à résoudre, on peut toujours mettre l'expression (h.p-k.q)2 en facteur. Celle-ci n'étant pas nulle, on peut alors la simplifier et on obtient la résolvante paramétrique de Sotta :
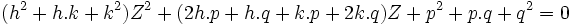
Donc le discriminant est ici :
![\Delta = -3(h.q - k.p)^2 = [i.\sqrt{3}(h.p - k.q)]^2 ~](https://static.techno-science.net/illustration/Definitions/autres/a/aa82346a079935a877b5fdba7326b344_14320feb513f364c112f53c0e326dc8a.png)
Les racines de la résolvante paramétrique sont alors :
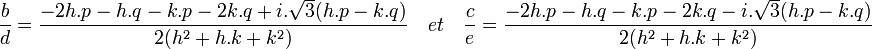
On peut choisir :
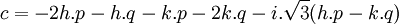
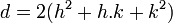
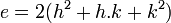
d'où :
![a = e^3a_2+3ce^2a_3 = -12(h.p - k.q).(h^2 + h.k + k^2)^2.[h^3 + 6h^2.k + 3h.k^2 - k^3 + i.(h^3 - 3h.k^2 - k^3).\sqrt{3}] ~](https://static.techno-science.net/illustration/Definitions/autres/0/07395e1b4e96b1c032672c8b884574c1_92e0fa7a2ecf9b8567d63230c3a06fd4.png)
![f = d^3a_2+3bd^2a_3 = -12(h.p - k.q).(h^2 + h.k + k^2)^2.[h^3 + 6h^2.k + 3h.k^2 - k^3 - i.(h^3 - 3h.k^2 - k^3).\sqrt{3}] ~](https://static.techno-science.net/illustration/Definitions/autres/8/8e8098de6446ebcaa1920c802444f56b_1bb03acfb9374cf2ee20db91fc7b2e70.png)
Nous voyons a ce niveau, que l'on peut faire apparaître une exponentielle complexe dans a et f en rendant a et f respectivement proportionnel à
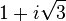
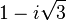
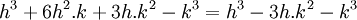
Qui après simplification nous donne la relation :
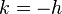
En s'inspirant de l'exemple 4, nous voyons aussi qu'il serait souhaitable que b et c soit égal ou opposé. Comme b et c sont deux nombres complexes conjugués, il suffit d'annuler leur partie réelle ou imaginaire. Compte tenu de la condition h.p - k.q non nulle, nous ne pouvons pas annuler la partie imaginaire. Nous annulerons donc la partie réelle :
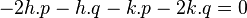
Qui compte tenu de la première relation déjà trouvé k = -h nous donne la seconde relation :
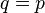
Le changement de variable initial devient alors :
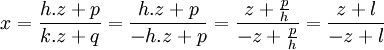
En posant :
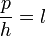
Et nous remarquons que nous n'avons plus qu'un paramètre l à déterminer.
Le plus simple est de tout recommencer.
En posant :
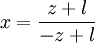
dans
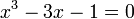
On obtient :
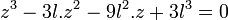
Calculons la résolvante paramétrique. On obtient :
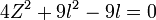
Qui a pour racine :
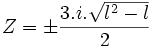
On peut choisir :
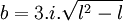
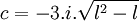
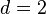
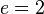
D'où :
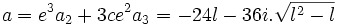
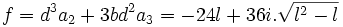
Si l'on veut que a et f soit proportionnel respectivement à :
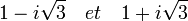
Il faut que :
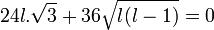
Ce qui entraîne :
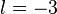
Le changement de variable à faire était donc :
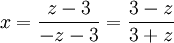
Avec ce changement de variable, nous obtenons :
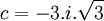
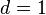
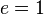
D'où :
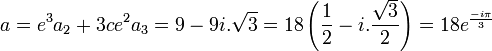
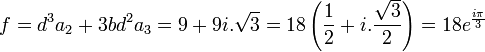
On obtient donc les trois racines suivantes:
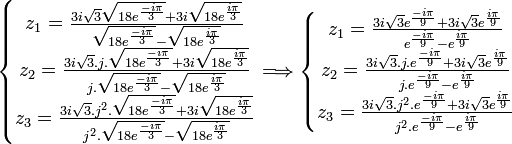
Et en procédant comme dans l'exemple 4, on obtient :
En portant ces valeurs de z dans :
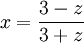
On obtient:
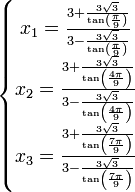
Et en simplifiant, on obtient finalement :