Méthode de Sotta - Définition

Méthode trigonométrique de Sotta en cosinus kpi/7

Soit à résoudre l'équation :

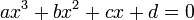
On choisit h et k tel que soit racine de l'une des deux équations suivantes (résolvantes trigonométriques en pi/7) :

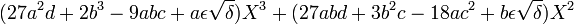
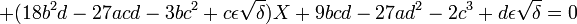
ε prenant successivement les valeurs ε = 1 et ε = -1.

On retiendra la valeur de ε qui fournit une résolvante trigonométrique ayant une racine la plus simple possible (le plus souvent une racine évidente). si aucune des deux valeurs de ε ne permet d'avoir une racine s'exprimant simplement, on peut considérer que la méthode a échoué.

On choisit ensuite p et q tel que :

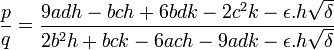
On pose ensuite :

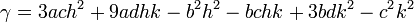
Les racines de l'équation à résoudre sont alors :

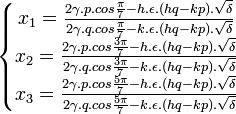
Méthode trigonométrique de Sotta en cosinus kpi/9

Soit à résoudre l'équation :

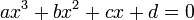
On choisit h et k tel que soit racine de l'une des deux équations suivantes (résolvantes trigonométriques en pi/9) :

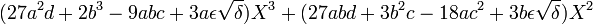
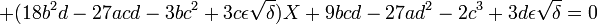
ε prenant successivement les valeurs ε = 1 et ε = -1.

On retiendra la valeur de ε qui fournit une résolvante trigonométrique ayant une racine la plus simple possible (le plus souvent une racine évidente). si aucune des deux valeurs de ε ne permet d'avoir une racine s'exprimant simplement, on peut considérer que la méthode a échoué.

On choisit ensuite p et q tel que :

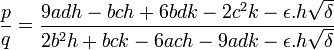
On pose ensuite :

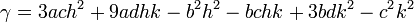
Les racines de l'équation à résoudre sont alors :

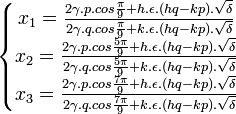
Autres méthodes de résolution d'équations

• Méthode de Tschirnhaus
• Méthode de Bézout
• Méthode de Cardan
• Méthode de Ferrari
• Méthode de Descartes
• Méthode d'Hermite