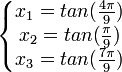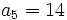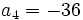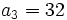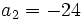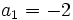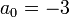Méthode de Sotta - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Principe de la méthode - Application à la résolution des équations de degré 4 - Application à la résolution des équations de degré 3 - Application à la résolution des équations de degré 6 - Application à la résolution des équations de degré 5 - Cas général - Application à la résolution des équations de degré 7 - Équations dont l'équation résolvante admet une racine nulle - Compléments - Exemples - Équations dont l'équation résolvante admet une racine double - Méthodes trigonométriques de Sotta - Méthode paramétrique de Sotta - Méthode trigonométrique de Sotta en tangente kpi/7 - Méthode trigonométrique de Sotta en tangente kpi/9 - Méthode trigonométrique de Sotta en cosinus kpi/7 - Méthode trigonométrique de Sotta en cosinus kpi/9 - Autres méthodes de résolution d'équations

Compléments

Ce paragraphe examine plus en détail, pour n > 3, le cas où la résolvante n'est pas du second degré. C'est-à-dire si :

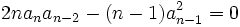
$2na_na_{n-2}-(n-1)a_{n-1}^2 = 0 ~$

En fait, cette condition entraîne que tous les coefficients de l'équation résolvante sont nuls.

Nous présentons la démonstration pour les équations du cinquième degré. Mais cette démonstration est aisément adaptable aux autres degrés.

Supposons donc que le coefficient du second degré de l'équation résolvante soit nul :

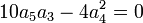
$10a_5a_3-4a_4^2 = 0 ~$

Nous remarquons que la première condition de résolubilité :

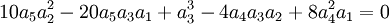
$10a_5a_2^2-20a_5a_3a_1+a_3^3-4a_4a_3a_2+8a_4^2a_1=0 ~$

peut s'écrire sous la forme :

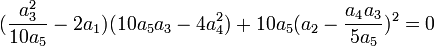
$(\frac{a_3^2}{10a_5} - 2a_1)(10a_5a_3-4a_4^2) + 10a_5(a_2 - \frac{a_4a_3}{5a_5})^2 = 0 ~$

Ce qui compte tenu de l'hypothèse :

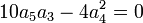
$10a_5a_3-4a_4^2 = 0 ~$

entraîne :

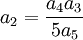
$a_2 = \frac{a_4a_3}{5a_5} ~$

Ce qui s'écrit :

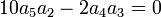
$10a_5a_2 - 2a_4a_3 = 0 ~$

Ce qui montre que le coefficient de degré 1 est nul

Calculons ensuite le coefficient du terme de degré 0 de l'équation résolvante :

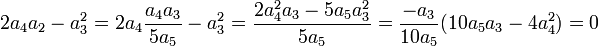
$2a_4a_2 - a_3^2 = 2a_4\frac{a_4a_3}{5a_5} - a_3^2 = \frac{2a_4^2a_3 - 5a_5a_3^2}{5a_5} = \frac{-a_3}{10a_5}(10a_5a_3 - 4a_4^2) = 0$

Nous avons bien démontré que tous les coefficients de l'équation résolvante sont nuls.

Nous avons alors deux possibilités.

Premier cas : Tous les coefficients de l'équation à résoudre ne sont pas nuls.

Alors l'équation à résoudre se met sous la forme :

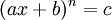
$(ax + b)^n = c ~$

Nous présentons la démonstration pour les équations du cinquième degré. Mais cette démonstration est aisément adaptable aux autres degrés.

Soit l'équation à résoudre :

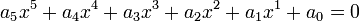
$a_5x^5 + a_4x^4 + a_3x^3 + a_2x^2 + a_1x^1 + a_0 = 0 ~$

Vérifiant ses deux conditions de résolubilités et dont tous les coefficients de l'équation résolvante sont nuls.

Posons :

$a_3 = t ~$

$a_4 = s ~$

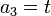
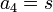
Avec s et t non nuls puisque tous les coefficients de l'équation à résoudre sont non nuls.

La condition :

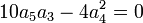
$10a_5a_3 - 4a_4^2 = 0 ~$

entraîne :

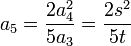
$a_5 = \frac{2a_4^2}{5a_3} = \frac{2s^2}{5t} ~$

La condition :

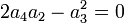
$2a_4a_2 - a_3^2 = 0 ~$

entraîne :

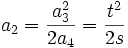
$a_2 = \frac{a_3^2}{2a_4} = \frac{t^2}{2s} ~$

La condition :

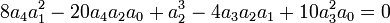
$8a_4a_1^2-20a_4a_2a_0+a_2^3-4a_3a_2a_1+10a_3^2a_0=0 ~$

S'écrit en remplaçant ce qui est connue :

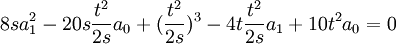
$8sa_1^2-20s\frac{t^2}{2s}a_0+(\frac{t^2}{2s})^3-4t\frac{t^2}{2s}a_1+10t^2a_0 = 0 ~$

Qui se simplifie sous la forme :

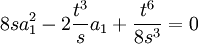
$8sa_1^2 - 2\frac{t^3}{s}a_1 + \frac{t^6}{8s^3} = 0 ~$

En multipliant par 8s³, on obtient :

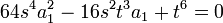
$64s^4a_1^2 - 16s^2t^3a_1 + t^6 = 0 ~$

Cette expression se factorise sous la forme :

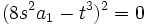
$(8s^2a_1 - t^3)^2 = 0 ~$

D'où l'on déduit :

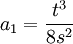
$a_1 = \frac{t^3}{8s^2} ~$

En reportant tous les coefficients que l'on a calculés dans l'équation à résoudre, on obtient :

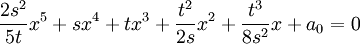
$\frac{2s^2}{5t}x^5 + sx^4 + tx^3 + \frac{t^2}{2s}x^2 + \frac{t^3}{8s^2}x + a_0 = 0 ~$

En multipliant tous les termes par :

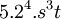
$5.2^4.s^3t ~$

On obtient :

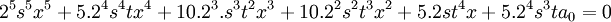
$2^5s^5x^5 + 5.2^4s^4tx^4 + 10.2^3.s^3t^2x^3 + 10.2^2s^2t^3x^2 + 5.2st^4x + 5.2^4s^3ta_0 = 0 ~$

Qui peut s'écrire sous la forme :

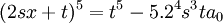
$(2sx + t)^5 = t^5 - 5.2^4s^3ta_0 ~$

En posant :

$a = 2s ~$

$b = t ~$

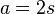
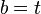
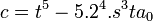
$c = t^5 - 5.2^4.s^3ta_0 ~$

Nous voyons que l'équation à résoudre se met bien sous la forme :

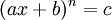
Et l'on en déduit les n racines :

$x_k = \frac{1}{a}\left(e^{\frac{2ki\pi}{n}}\sqrt[n]{c} - b \right) ~$

Avec k prenant successivement toutes les valeurs entières de 0 à n-1

Deuxième cas : Certains coefficients de l'équation à résoudre sont nuls.

La méthode ne permet pas, en général, d'aboutir.

L'équation peut même être non résoluble par radicaux comme c'est le cas des équations du type :

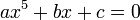
$ax^5 + bx + c = 0 ~$

Dont on démontre qu'elles ne sont pas en général résolubles par radicaux pour b différent de 0.

Exemples

Les deux premiers exemples qui suivent ont été choisis de façon à ce que l'équation résolvante ait un discriminant sous forme de carré parfait afin de simplifier les calculs. Mais la méthode s'applique aussi bien lorsque le discriminant n'est pas un carré parfait, est négatif (Exemples 3 et 4), ou est un nombre complexe quelconque.

Exemple 1

Soit à résoudre l'équation :

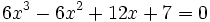
$\qquad 6x^3 - 6x^2 + 12x + 7 = 0$

La résolvante de Sotta est :

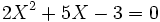
$\qquad 2X^2 + 5X - 3 = 0$

qui a pour racine :

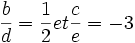
$\qquad \frac{b}{d} = \frac{1}{2} et \frac{c}{e} = -3$

On peut choisir :

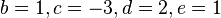
$\qquad b = 1, c = -3, d = 2, e = 1$

d'où :

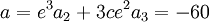
$\qquad a = e^3a_2+3ce^2a_3 = -60$

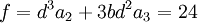
$\qquad f = d^3a_2+3bd^2a_3 = 24$

En posant :

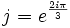
$\qquad j = e^{\frac{2i\pi}{3}}$

On obtient les trois racines suivantes :

$\qquad x_1 = \frac{\sqrt[3]{-60} - (-3)\sqrt[3]{24}}{2\sqrt[3]{-60} - \sqrt[3]{24}} = \frac{\sqrt[3]{5} - 3\sqrt[3]{2}}{2\sqrt[3]{5} + \sqrt[3]{2}}$

$\qquad x_2 = \frac{j\sqrt[3]{-60} - (-3)\sqrt[3]{24}}{2j\sqrt[3]{-60} - \sqrt[3]{24}} = \frac{j\sqrt[3]{5} - 3\sqrt[3]{2}}{2j\sqrt[3]{5} + \sqrt[3]{2}}$

$\qquad x_3 = \frac{j^2\sqrt[3]{-60} - (-3)\sqrt[3]{24}}{2j^2\sqrt[3]{-60} - \sqrt[3]{24}} = \frac{j^2\sqrt[3]{5} - 3\sqrt[3]{2}}{2j^2\sqrt[3]{5} + \sqrt[3]{2}}$

Exemple 2

Soit à résoudre l'équation :

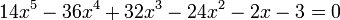
$\qquad 14x^5 - 36x^4 + 32x^3 - 24x^2 - 2x - 3 = 0$

On a alors :

$\qquad a_5 = 14$
$\qquad a_4 = -36$
$\qquad a_3 = 32$
$\qquad a_2 = -24$
$\qquad a_1 = -2$
$\qquad a_0 = -3$

Pour savoir si l'équation est résoluble par la méthode de Sotta, nous devons vérifier les conditions de résolubilité.

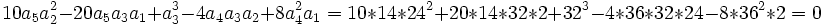
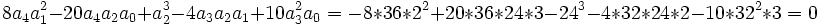
$\qquad 10a_5a_2^2-20a_5a_3a_1+a_3^3-4a_4a_3a_2+8a_4^2a_1=10*14*24^2+20*14*32*2+32^3-4*36*32*24-8*36^2*2=0$ $\qquad 8a_4a_1^2-20a_4a_2a_0+a_2^3-4a_3a_2a_1+10a_3^2a_0=-8*36*2^2+20*36*24*3-24^3-4*32*24*2-10*32^2*3=0$

La résolvante de Sotta est :

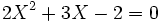
$\qquad 2X^2 + 3X - 2=0$

qui a pour racine :

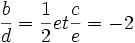
$\qquad \frac{b}{d} = \frac{1}{2} et \frac{c}{e} = -2$

On peut choisir :

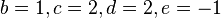
$\qquad b = 1, c = 2, d = 2, e = -1$

d'où :

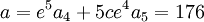
$\qquad a = e^5a_4+5ce^4a_5 = 176$

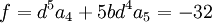
$\qquad f = d^5a_4+5bd^4a_5 = -32$

L'une des racines de l'équation sera :

$\qquad x_1 = \frac{\sqrt[5]{176} - 2\sqrt[5]{-32}}{2\sqrt[5]{176} - (-1)\sqrt[5]{-32}} = \frac{\sqrt[5]{11} + 2\sqrt[5]{2}}{2\sqrt[5]{11} - \sqrt[5]{2}}$

On obtient alors les cinq racines suivantes :

$\qquad x_1 = \frac{\sqrt[5]{11} + 2\sqrt[5]{2}}{2\sqrt[5]{11} - \sqrt[5]{2}}$

$\qquad x_2 = \frac{e^{\frac{2i\pi}{5}}\sqrt[5]{11} + 2\sqrt[5]{2}}{2e^{\frac{2i\pi}{5}}\sqrt[5]{11} - \sqrt[5]{2}}$

$\qquad x_3 = \frac{e^{\frac{4i\pi}{5}}\sqrt[5]{11} + 2\sqrt[5]{2}}{2e^{\frac{4i\pi}{5}}\sqrt[5]{11} - \sqrt[5]{2}}$

$\qquad x_4 = \frac{e^{\frac{6i\pi}{5}}\sqrt[5]{11} + 2\sqrt[5]{2}}{2e^{\frac{6i\pi}{5}}\sqrt[5]{11} - \sqrt[5]{2}}$

$\qquad x_5 = \frac{e^{\frac{8i\pi}{5}}\sqrt[5]{11} + 2\sqrt[5]{2}}{2e^{\frac{8i\pi}{5}}\sqrt[5]{11} - \sqrt[5]{2}}$

Exemple 3

Soit à résoudre l'équation :

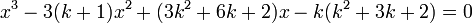
$x^3 - 3(k + 1)x^2 + (3k^2 + 6k + 2)x - k(k^2 + 3k + 2) = 0 ~$

Donc les coefficients dépendent d'un paramètre k.

La résolvante de Sotta est :

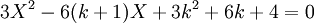
$3X^2 - 6(k + 1)X + 3k^2 + 6k + 4 = 0 ~$

Donc le discriminant est :

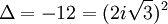
$\Delta = -12 = (2i\sqrt{3})^2 ~$

et qui a donc pour racine :

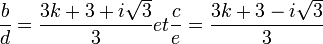
$\qquad \frac{b}{d} = \frac{3k + 3 + i \sqrt{3}}{3} et \frac{c}{e} = \frac{3k + 3 - i \sqrt{3}}{3}$

On peut choisir :

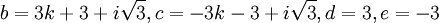
$b = 3k + 3 + i \sqrt{3}, c = -3k - 3 + i \sqrt{3}, d = 3, e = -3 ~$

d'où :

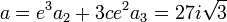
$a = e^3a_2+3ce^2a_3 = 27i\sqrt{3} ~$

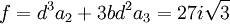
$f = d^3a_2+3bd^2a_3 = 27i\sqrt{3} ~$

En posant :

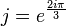
$j = e^{\frac{2i\pi}{3}} ~$

On obtient les trois racines suivantes :

$\left\{\begin{matrix} x_1 = \frac{(3k+3+i\sqrt{3})\sqrt[3]{27i\sqrt{3}} - (-3k-3+i\sqrt{3})\sqrt[3]{27i\sqrt{3}}}{3\sqrt[3]{27i\sqrt{3}} + 3\sqrt[3]{27i\sqrt{3}}} \\ x_2 = \frac{(3k+3+i\sqrt{3})j\sqrt[3]{27i\sqrt{3}} - (-3k-3+i\sqrt{3})\sqrt[3]{27i\sqrt{3}}}{3j\sqrt[3]{27i\sqrt{3}} + 3\sqrt[3]{27i\sqrt{3}}} \\ x_3 = \frac{(3k+3+i\sqrt{3})j^2\sqrt[3]{27i\sqrt{3}} - (-3k-3+i\sqrt{3})\sqrt[3]{27i\sqrt{3}}}{3j^2\sqrt[3]{27i\sqrt{3}} + 3\sqrt[3]{27i\sqrt{3}}} \end{matrix}\right.$

En simplifiant le numérateur et le dénominateur de chaque fraction par :

$\sqrt[3]{27i\sqrt{3}} ~$

Et en remarquant que :

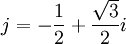
$j = -\frac{1}{2} + \frac{\sqrt{3}}{2}i ~$

On obtient :

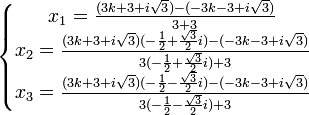
$\left\{\begin{matrix} x_1 = \frac{(3k+3+i\sqrt{3}) - (-3k-3+i\sqrt{3})}{3 + 3} \\ x_2 = \frac{(3k+3+i\sqrt{3})(-\frac{1}{2} + \frac{\sqrt{3}}{2}i) - (-3k-3+i\sqrt{3})}{3(-\frac{1}{2} + \frac{\sqrt{3}}{2}i) + 3} \\ x_3 = \frac{(3k+3+i\sqrt{3})(-\frac{1}{2} - \frac{\sqrt{3}}{2}i) - (-3k-3+i\sqrt{3})}{3(-\frac{1}{2} - \frac{\sqrt{3}}{2}i) + 3} \end{matrix}\right.$

En développant et en multipliant éventuellement le numérateur et le dénominateur de chaque fraction par 2, on obtient :

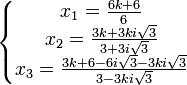
$\left\{\begin{matrix} x_1 = \frac{6k + 6}{6} \\ x_2 = \frac{3k + 3ki\sqrt{3}}{3 + 3i\sqrt{3}} \\ x_3 = \frac{3k + 6 - 6i\sqrt{3} - 3ki\sqrt{3}}{3 - 3ki\sqrt{3}} \end{matrix}\right.$

En multipliant éventuellement le numérateur et le dénominateur de chaque fraction par l'expression conjuguée du dénominateur correspondant, on obtient finalement :

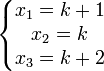
$\left\{\begin{matrix} x_1 = k + 1 \\ x_2 = k \\ x_3 = k + 2 \end{matrix}\right.$

Exemple 4

Soit à résoudre l'équation :

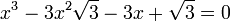
$x^3 - 3x^2\sqrt{3} - 3x + \sqrt{3} = 0 ~$

La résolvante de Sotta est :

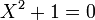
$\qquad X^2 + 1 = 0$

qui a pour racine :

$\qquad \frac{b}{d} = i et \frac{c}{e} = -i$

On peut choisir :

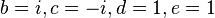
$\qquad b = i, c = -i, d = 1, e = 1$

d'où :

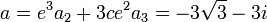
$\qquad a = e^3a_2+3ce^2a_3 = -3\sqrt{3} - 3i$

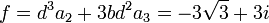
$\qquad f = d^3a_2+3bd^2a_3 = -3\sqrt{3} + 3i$

En posant :

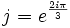
$\qquad j = e^{\frac{2i\pi}{3}}$

On obtient les trois racines suivantes :

$\left\{\begin{matrix} x_1 = \frac{i\sqrt[3]{-3\sqrt{3} - 3i} - (-i)\sqrt[3]{-3\sqrt{3} + 3i}}{\sqrt[3]{-3\sqrt{3} - 3i} - \sqrt[3]{-3\sqrt{3} + 3i}} \\ x_2 = \frac{ij\sqrt[3]{-3\sqrt{3} - 3i} - (-i)\sqrt[3]{-3\sqrt{3} + 3i}}{j\sqrt[3]{-3\sqrt{3} - 3i} - \sqrt[3]{-3\sqrt{3} + 3i}} \\ x_3 = \frac{ij^2\sqrt[3]{-3\sqrt{3} - 3i} - (-i)\sqrt[3]{-3\sqrt{3} + 3i}}{j^2\sqrt[3]{-3\sqrt{3} - 3i} - \sqrt[3]{-3\sqrt{3} + 3i}} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} x_1 = \frac{i\sqrt[3]{\frac{\sqrt{3}}{2} + \frac{1}{2}i} + i\sqrt[3]{\frac{\sqrt{3}}{2} - \frac{1}{2}i}}{\sqrt[3]{\frac{\sqrt{3}}{2} + \frac{1}{2}i} - \sqrt[3]{\frac{\sqrt{3}}{2} - \frac{1}{2}i}} \\ x_2 = \frac{ij\sqrt[3]{\frac{\sqrt{3}}{2} + \frac{1}{2}i} + i\sqrt[3]{\frac{\sqrt{3}}{2} - \frac{1}{2}i}}{j\sqrt[3]{\frac{\sqrt{3}}{2} + \frac{1}{2}i} - \sqrt[3]{\frac{\sqrt{3}}{2} - \frac{1}{2}i}} \\ x_3 = \frac{ij^2\sqrt[3]{\frac{\sqrt{3}}{2} + \frac{1}{2}i} + i\sqrt[3]{\frac{\sqrt{3}}{2} - \frac{1}{2}i}}{j^2\sqrt[3]{\frac{\sqrt{3}}{2} + \frac{1}{2}i} - \sqrt[3]{\frac{\sqrt{3}}{2} - \frac{1}{2}i}} \end{matrix}\right. ~$

Comme :

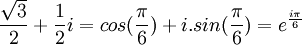
$\frac{\sqrt{3}}{2} + \frac{1}{2}i = cos(\frac{\pi}{6}) + i.sin(\frac{\pi}{6}) = e^{\frac{i\pi}{6}} ~$

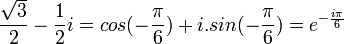
$\frac{\sqrt{3}}{2} - \frac{1}{2}i = cos(-\frac{\pi}{6}) + i.sin(-\frac{\pi}{6}) = e^{-\frac{i\pi}{6}} ~$

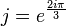
$j = e^{\frac{2i\pi}{3}} ~$

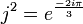
$j^2 = e^{\frac{-2i\pi}{3}} ~$

On obtient :

$\left\{\begin{matrix} x_1 = \frac{i\sqrt[3]{e^{\frac{i\pi}{6}}} + i\sqrt[3]{e^{-\frac{i\pi}{6}}}}{\sqrt[3]{e^{\frac{i\pi}{6}}} - \sqrt[3]{e^{-\frac{i\pi}{6}}}} \\ x_2 = \frac{i.e^{\frac{2i\pi}{3}}\sqrt[3]{e^{\frac{i\pi}{6}}} + i\sqrt[3]{e^{-\frac{i\pi}{6}}}}{e^{\frac{2i\pi}{3}}\sqrt[3]{e^{\frac{i\pi}{6}}} - \sqrt[3]{e^{-\frac{i\pi}{6}}}} \\ x_3 = \frac{i.e^{\frac{-2i\pi}{3}}\sqrt[3]{e^{\frac{i\pi}{6}}} + i\sqrt[3]{e^{-\frac{i\pi}{6}}}}{e^{\frac{-2i\pi}{3}}\sqrt[3]{e^{\frac{i\pi}{6}}} - \sqrt[3]{e^{-\frac{i\pi}{6}}}} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} x_1 = \frac{ie^{\frac{i\pi}{18}} + ie^{-\frac{i\pi}{18}}}{e^{\frac{i\pi}{18}} - e^{-\frac{i\pi}{18}}} \\ x_2 = \frac{i.e^{\frac{13i\pi}{18}} + ie^{-\frac{i\pi}{18}}}{e^{\frac{13i\pi}{18}} - e^{-\frac{i\pi}{18}}} \\ x_3 = \frac{ie^{\frac{-11i\pi}{18}} + ie^{-\frac{i\pi}{18}}}{e^{\frac{-11i\pi}{18}} - e^{-\frac{i\pi}{18}}} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} x_1 = \frac{i(e^{\frac{i\pi}{18}} + e^{-\frac{i\pi}{18}})}{e^{\frac{i\pi}{18}} - e^{-\frac{i\pi}{18}}} \\ x_2 = \frac{i(e^{\frac{13i\pi}{18}} + e^{-\frac{i\pi}{18}})e^{\frac{-6i\pi}{18}}}{(e^{\frac{13i\pi}{18}} - e^{-\frac{i\pi}{18}})e^{\frac{-6i\pi}{18}}} \\ x_3 = \frac{i(e^{\frac{-11i\pi}{18}} + e^{-\frac{i\pi}{18}})e^{\frac{6i\pi}{18}}}{(e^{\frac{-11i\pi}{18}} - e^{-\frac{i\pi}{18}})e^{\frac{6i\pi}{18}}} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} x_1 = \frac{i(e^{\frac{i\pi}{18}} + e^{-\frac{i\pi}{18}})}{e^{\frac{i\pi}{18}} - e^{-\frac{i\pi}{18}}} \\ x_2 = \frac{i(e^{\frac{7i\pi}{18}} + e^{\frac{-7i\pi}{18}})}{e^{\frac{7i\pi}{18}} - e^{\frac{-7i\pi}{18}}} \\ x_3 = \frac{i(e^{\frac{-5i\pi}{18}} + e^{\frac{5i\pi}{18}})}{e^{\frac{-5i\pi}{18}} - e^{\frac{5i\pi}{18}}} \end{matrix}\right. ~$

Compte tenue des formules d'Euler :

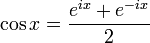
$\cos x = {e^{ix} + e^{-ix} \over 2} ~$

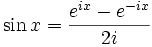
$\sin x = {e^{ix} - e^{-ix} \over 2i} ~$

On obtient :

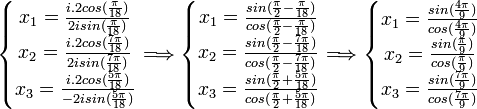
$\left\{\begin{matrix} x_1 = \frac{i.2cos( \frac{\pi}{18} )}{2isin(\frac{\pi}{18})} \\ x_2 = \frac{i.2cos( \frac{7\pi}{18} )}{2isin(\frac{7\pi}{18})} \\ x_3 = \frac{i.2cos( \frac{5\pi}{18} )}{-2isin(\frac{5\pi}{18})} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} x_1 = \frac{sin( \frac{\pi}{2} - \frac{\pi}{18} )}{cos(\frac{\pi}{2} - \frac{\pi}{18})} \\ x_2 = \frac{sin(\frac{\pi}{2} - \frac{7\pi}{18} )}{cos(\frac{\pi}{2} - \frac{7\pi}{18})} \\ x_3 = \frac{sin(\frac{\pi}{2} + \frac{5\pi}{18} )}{cos(\frac{\pi}{2} + \frac{5\pi}{18})} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} x_1 = \frac{sin(\frac{4\pi}{9} )}{cos(\frac{4\pi}{9})} \\ x_2 = \frac{sin(\frac{\pi}{9} )}{cos(\frac{\pi}{9})} \\ x_3 = \frac{sin(\frac{7\pi}{9} )}{cos(\frac{7\pi}{9})} \end{matrix}\right. ~$

On obtient donc finalement :

$\left\{\begin{matrix} x_1 = tan(\frac{4\pi}{9}) \\ x_2 = tan(\frac{\pi}{9}) \\ x_3 = tan(\frac{7\pi}{9}) \end{matrix}\right. ~$

Équations dont l'équation résolvante admet une racine nulle

Équations dont l'équation résolvante admet une racine double

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Page générée en 0.138 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise