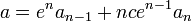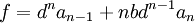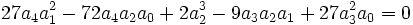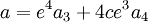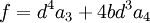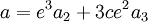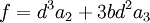Méthode de Sotta - Définition

Introduction

La méthode de Sotta, imaginée et mise au point par Bernard Sotta, permet de résoudre toutes les équations du troisième degré et peut se généraliser à certaines équations de degré supérieur ou égal à 4 si les coefficients de ces équations vérifient certaines conditions.

Ces équations fournissent des exemples d'équations qui, bien qu'ayant un degré supérieur ou égal à 5, ont un groupe de Galois résoluble. Nous savons en effet que les équations de degré supérieur ou égal à 5 n'ont pas forcément un groupe de Galois résoluble. Ce qui permet d'affirmer qu'il n'existe pas de méthode générale pour les résoudre. (voir Théorie de Galois).

Principe de la méthode

Dans tout cet article n est un nombre entier représentant le degré de l'équation à résoudre.

Toutes les autres lettres représentent des nombres complexes.

Par convention désigne n'importe laquelle des n racines n^ème de a, il en est de même de

Considérons une équation de degré n avec n > 2 :

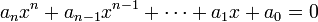
Vérifiant les deux conditions :

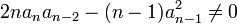
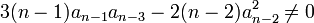
Ces deux conditions permettent de garantir que l'équation résolvante définie ci-dessous existe et n'a pas de racines nulles.

Nous supposerons par la suite que ces conditions sont vérifiées sauf indications contraires.

Nous appellerons équation résolvante de Sotta associée à l'équation précédente, l'équation du second degré suivante :

Nous avons alors le théorème suivant (théorème de Sotta) :

Si l'équation :

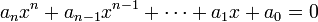
admet des racines sous la forme :

(d et e non nul).

alors et sont les deux racines de l'équation résolvante.

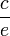
a et f sont alors donné par les deux relations :

• 
• 

Les n racines de l'équation proposée seront alors :

avec k prenant successivement toutes les valeurs entières de 0 à n-1

Sauf précision contraire, les paragraphes suivants supposent que l'équation résolvante n'admet pas une racine double. Le cas particulier où l'équation résolvante admet une racine double est traité plus loin.

Application à la résolution des équations de degré 4

Les équations de degré 4 :

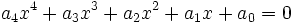
admettent des racines sous la forme :

seulement si :

• 

Par conséquent, la méthode de Sotta ne permet de résoudre que les équations de degré 4 vérifiant cette condition de résolubilité.

Soit donc l'équation suivante :

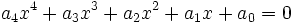
Premier cas : Si (condition pour que la résolvante soit du second degré).

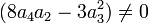
La résolvante de Sotta associée sera :

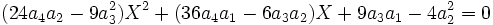
Il suffit donc de choisir b, c, d, e tel que et soit les racines de la résolvante. On calcule ensuite a et f à l'aide des formules :

• 
• 

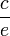
Les quatre racines de l'équation à résoudre seront :

avec k prenant successivement les valeurs 0, 1, 2, 3.

Deuxième cas : Si .

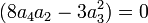
Voir le paragraphe en fin d'article.

Application à la résolution des équations de degré 3

Toutes les équations de degré 3 ayant trois racines distinctes admettent des racines sous la forme :

par conséquent, la méthode de Sotta permet de résoudre toutes les équations de degré 3.

Soit donc l'équation suivante :

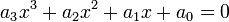
Premier cas : Si et (condition pour que la résolvante soit du second degré avec des racines non nulles).

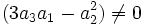
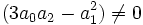
La résolvante de Sotta associée sera :

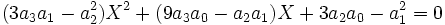
Il suffit donc de choisir b, c, d, e tel que et soit les racines de la résolvante. On calcule ensuite a et f à l'aide des formules :

• 
• 

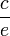
Les trois racines de l'équation à résoudre seront alors :

avec :

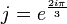
Remarque : Si l'équation résolvante admet une racine double α, celle-ci est aussi racine double de l'équation à résoudre et la troisième racine simple β manquante est obtenue par la relation :

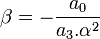
En effet, en désignant par α, β, γ, les trois racines de l'équation à résoudre, celle-ci peut se mettre sous la forme :

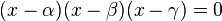
En développant le premier membre et en formant l'équation résolvante, on obtient une équation du second degré dont le discriminant Δ peut se factoriser sous la forme :

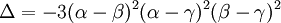
Si l'équation résolvante a une racine double, cela signifie que son discriminant Δ est nul. Nous voyons alors que cela n'est possible que si deux des nombres parmi α, β, γ sont égaux et on vérifie que cette valeur commune se trouve être justement la racine double de l'équation résolvante.

Inversement, on montre que si l'équation à résoudre admet une racine double, l'équation résolvante admet aussi la même racine double.

Deuxième cas : Si (On est dans le cas: d ou e nul)

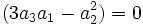
On multiplie par 3a₁a₂ tous les termes de l'équation :

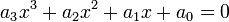
On obtient :

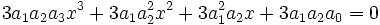
Comme :

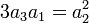
L'équation devient :

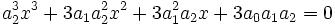
Qui se met sous la forme :

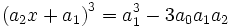
On en déduit les trois racines de l'équation à résoudre :

Troisième cas : Si (On est dans le cas: b ou c nul)

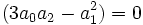
On multiplie par 3a₁a₂ tous les termes de l'équation :

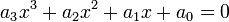
On obtient :

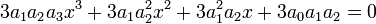
Comme :

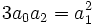
L'équation devient :

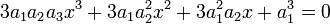
Divisons maintenant chaque terme par x³, on obtient :

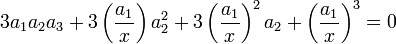
Qui se met sous la forme :

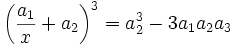
On en déduit les trois racines de l'équation à résoudre :