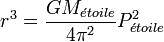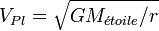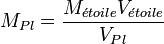Méthode des vitesses radiales - Définition

Méthode

Une série d'observations sont effectuées sur le spectre de la lumière émise par l'étoile. Des variations dans ce spectre peuvent être détectées, lorsque la longueur d'onde de certaines raies d'absorption spectrales augmente et diminue de façon régulière sur un intervalle de temps donné. Ces variations peuvent être révélatrices de changements dans la vitesse radiale, celle-ci pouvant être altérée par la présence d'une planète en orbite autour de l'étoile, causant l'effet Doppler-Fizeau sur la lumière émise par l'étoile.

Si une planète extrasolaire est détectée, sa masse peut être déterminée à partir des changements de vitesse radiale de son étoile. Un graphique de la vitesse radiale, mesurée par rapport au temps donnera une courbe caractéristique (courbe sinusoïdale dans le cas d'une orbite circulaire), et l'amplitude de la courbe permettra de calculer la masse de la planète.

Exemple

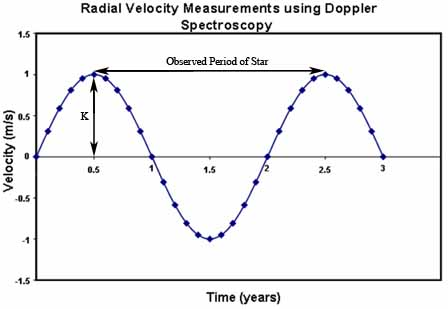
Le graphique à droite illustre la courbe sinusoïdale créée en utilisant la spectroscopie Doppler pour observer une étoile imaginaire autour de laquelle graviterait une planète sur une orbite circulaire. Des observations sur une étoile réelle engendrerait une graphe similaire, bien que l'excentricité orbitale déformerait la courbe et compliquerait les calculs ci-dessous.

La vitesse de l'étoile théorique montre une variation périodique de ± 1 m/s, suggérant une masse qui est en orbite autour d'elle.En utilisant la troisième loi de Kepler, la période observée de l'orbite de la planète autour de l'étoile (correspondant à la période à laquelle le spectre de l'étoile se modifie) peut être utilisée afin de déterminer la distance séparant la planète de l'étoile. Ceci peut se faire grâce à l'équation suivante :

où

• r est la distance séparant la planète de l'étoile,
• G est la constante gravitationnelle,
• M_etoile est la masse de l'étoile,
• P_etoile est la période citée plus haute.

Ayant à présent déterminé r, la vélocité de la planète autour de l'étoile peut être calculée en utilisant la loi de Newton sur la gravitation :

où V_Pl est la vélocité de la planète.

La masse de la planète peut alors être calculée à partir de sa vélocité :

où V_etoile est la vélocité observée de l'étoile principale. La vélocité Doppler observée, K = V_etoilesin(i), où i est l'inclinaison de l'orbite de la planète par rapport à la ligne de visée.

Ainsi, en supposant qu'on ait une valeur pour l'inclinaison de la planète et pour la masse de l'étoile, les changements dans la vitesse radiale de l'étoile peuvent être utilisée pour calculer la masse d'une exoplanète.