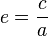Excentricité orbitale - Définition

Introduction

Exemples d'orbites caractérisées par différentes excentricités.

L’excentricité orbitale définit la forme des orbites des objets célestes. La forme générale est une ellipse, d'équation polaire (origine au foyer) : où e est l'excentricité. Elle donne ainsi une indication précise sur leur forme. Ainsi l'excentricité (e) est strictement définie pour toutes les orbites comme étant circulaire, elliptique, parabolique ou hyperbolique en prenant les valeurs suivantes :

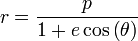
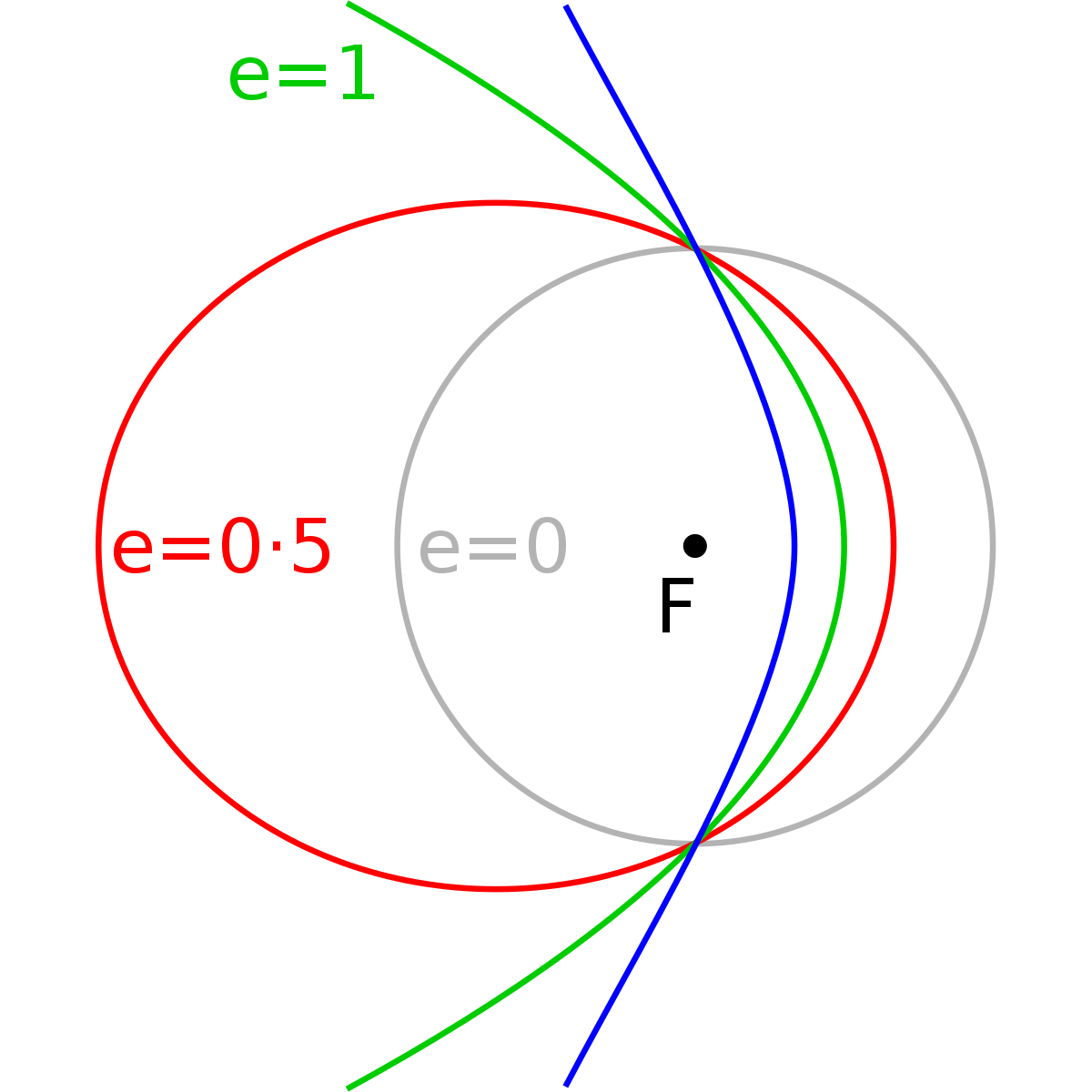
• pour les orbites circulaires : e = 0,
• pour les orbites elliptiques : 0 < e < 1,
• pour les trajectoires paraboliques : e = 1,
• pour les trajectoires hyperboliques : e > 1.

Comme les paraboles et les hyperboles ne sont pas des courbes fermées, on ne parle plus d'orbite mais de trajectoire.

Calcul de l'excentricité d'une orbite

Une ellipse avec ses axes, son centre, un foyer et la droite directrice associée . a est le demi grand-axe, b est le demi petit-axe, c est la distance entre le centre O de l'ellipse et un foyer F. Pour information h est la longueur séparant le foyer F de sa directrice (d) , et h = b² / c

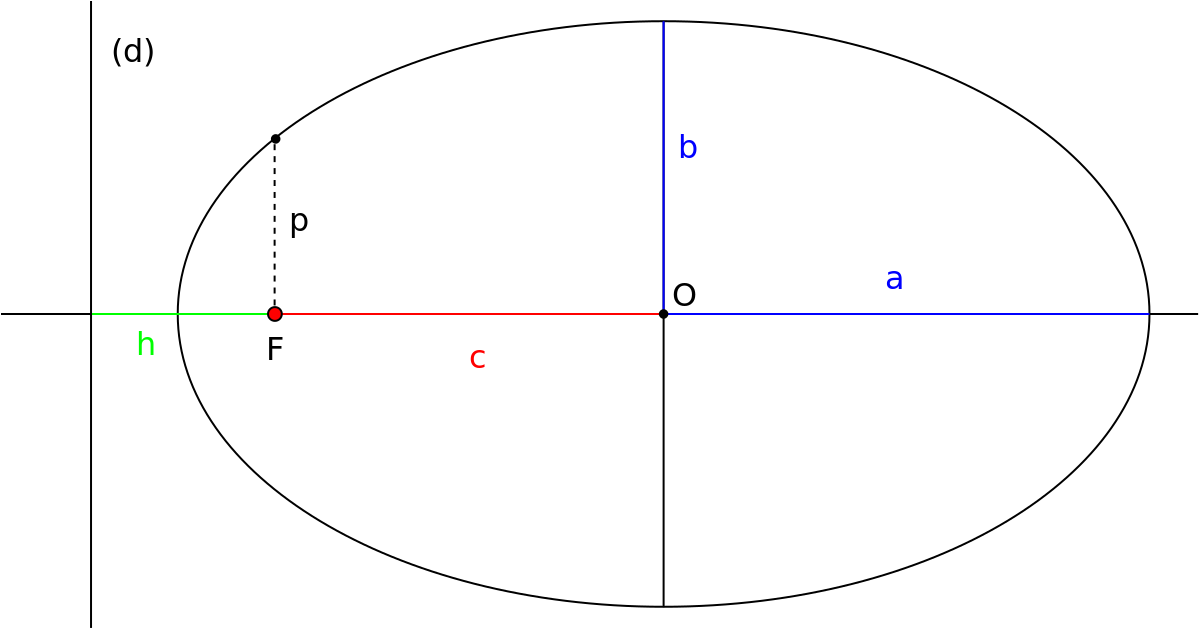
Pour les orbites elliptiques, l'excentricité d'une orbite pour être calculée en fonction de son apoapse et de son périapse :

,

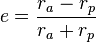
ce qui, après simplification, donne :

.

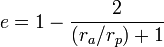
où :

• est le rayon à l'apoapse,
• est le rayon au périapse.

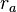
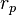
L'excentricité d'une orbite peut aussi se calculer de la façon suivante :

où:

• est la distance entre le centre de l'ellipse et un de ses deux foyers ; de plus ,
• est la longueur du demi grand-axe .

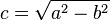
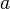
Phénomènes modifiant l'excentricité

Lorsque deux corps sont en orbite (révolution gravitationnelle) l'un autour de l'autre, l'excentricité des orbites est théoriquement fixée au départ et ne pourrait changer. En réalité, deux phénomènes principaux peuvent la modifier. D'une part, les deux astres ne sont pas isolés dans l'espace, et l'interaction des autres planètes et corps peuvent modifier l'orbite et par là même l'excentricité. Une autre modification, interne au système considéré, est due à l'effet de marée.

Prenons l'exemple concret de la Lune tournant autour de la Terre. Comme l'orbite de la Lune n'est pas circulaire, elle est soumise à des forces de marée, qui s'exercent différemment selon le point de l'orbite où se trouve la Lune, et varient continuement au cours de la révolution de la Lune. Les matériaux à l'intérieur de la Lune subissent donc des forces de friction, qui sont dissipatrices d'énergie, et qui tendent à rendre l'orbite circulaire, pour minimiser cette friction. En effet, l'orbite circulaire synchrone (la Lune montrant toujours la même face à la Terre) est l'orbite minimisant les variations des forces de marée.

→ Lorsque deux astres sont en rotation l'un autour de l'autre, l'excentricité des orbites a donc tendance à diminuer.

Dans un système type « planète/satellite » (corps de faible masse en rotation autour d'un corps de masse élevée), le temps nécessaire pour atteindre l'orbite circulaire (temps de « circularisation ») est beaucoup plus élevé que le temps nécessaire pour que le satellite présente toujours la même face à la planète (temps de « synchronisation »). La Lune présente ainsi toujours la même face à la Terre, sans que son orbite soit circulaire.

L'excentricité de l'orbite terrestre est, elle aussi, variable sur de très longues périodes (en centaines de millions d'années), essentiellement par interaction avec les autres planètes. La valeur actuelle est d'environ 0,0167, mais dans le passé elle a déjà atteint une valeur maximale de 0,07.