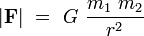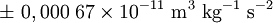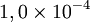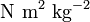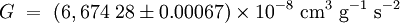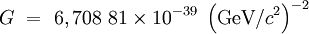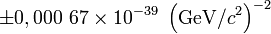Constante gravitationnelle - Définition

Introduction

En physique, la constante de proportionnalité de la loi de la gravitation est notée , et est appelée constante gravitationnelle, ou constante universelle de gravitation, ou constante de Newton, ou plus simplement grand G.

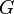
La constante gravitationnelle est une constante physique fondamentale qui apparaît dans la loi d'Isaac Newton sur la gravitation universelle et les lois qui en découlent (Lois de Képler,..).

La constante gravitationnelle apparaît aussi dans la théorie de la relativité générale d'Albert Einstein.

La force d'attraction entre deux corps massifs est proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance qui sépare leurs centres de masse respectifs.

Valeur

La constante gravitationnelle est une constante de proportionnalité de la force de gravitation c'est-à-dire d'attraction entre les corps; elle suit la loi en carré inverse des distances et est proportionnelle au produit des masses m₁ et m₂.

Valeur dans le SI

correspond à la force entre deux masses d'un kilogramme chacune, distantes d'un mètre.

Dans les unités SI, le CODATA de 2006 recommande la valeur suivante :

,

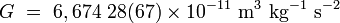
les chiffres entre parenthèses donnant la valeur de l'incertitude standard, qui est de :

Soit une incertitude relative de :

En termes dimensionnels, on peut également exprimer cette constante en :

Une autre estimation qui fait autorité est donnée par l'Union astronomique internationale (Standish 1995).

Valeur CGS

Dans le système CGS la valeur de la constante est :

Valeur GeV/c²

Avec une incertitude standard de :

Valeur en unités naturelles

Dans les unités dites « naturelles », et les autres constantes physiques comme la vitesse de la lumière , ont une valeur de 1.

Mesures de la constante gravitationnelle

La constante gravitationnelle est l'une des constantes les plus difficiles à mesurer.

a été mesurée directement la première fois par Henry Cavendish (Philosophical Transactions, 1798). Il utilisa une balance de torsion avec deux boules en mercure placées le long d'une tige horizontale. L'inertie des boules (reliée à la constante de torsion) permet de calculer la fréquence des oscillations de la balance. La très faible attraction causée par deux autres boules, placées indépendamment à l'extrémité de la tige, cause une légère modification des oscillations, et permet de calculer la force de gravité entre les boules, et ainsi la valeur de la constante de gravitation. Cavendish trouve . Cependant, son but n'était pas de mesurer cette constante, mais de mesurer la masse de la Terre.

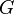
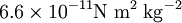
La précision de la valeur mesurée de a peu changé depuis cette première expérience. Cela est dû, non seulement à la faiblesse de la force de gravitation, mais aussi à l'impossibilité de s'affranchir réellement de la présence d'autres objets massifs (comme les murs du laboratoire...). Une très légère vibration du sol (provoquée par exemple par le passage d'un camion dans la rue) peut aussi compromettre la précision de la mesure. Une récente étude (Gillies, 1997) a montré que les valeurs publiées de la constante varient beaucoup, et que des mesures plus récentes et plus précises s'excluent mutuellement.

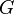
Historiquement l’existence de cette constante apparaît donc avec la loi de la gravitation de Newton mais ne pouvait constituer à ce stade qu’une hypothèse. La détermination de sa valeur a été réalisée à partir des expériences de Cavendish (1798). Les résultats de cette époque convergeaient vers une valeur unique (à des erreurs expérimentales acceptables près) démontrant par la même occasion l’existence de la constante. Cette constante associée à l’expression de Newton forme la formule de l’attraction universelle ,celle-ci verrait donc également ses bases également fragilisées. Cette formule, féconde, d’une grande simplicité de mise en œuvre, demeure utilisée sur des sujets actuels malgré l’avènement de la relativité.(exemple : hypothèse de la matière noire)