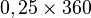Orbite - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
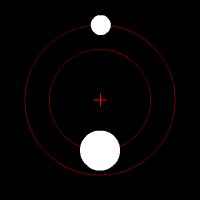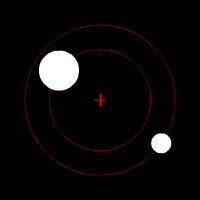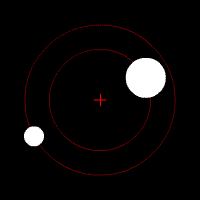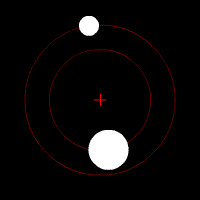
En mécanique céleste, une orbite est la trajectoire que dessine dans l'espace un corps autour d'un autre corps sous l'effet de la gravitation.
L'exemple classique est celui du système solaire où la Terre, les autres planètes, les astéroïdes et les comètes sont en orbite autour du Soleil. De même, des planètes possèdent des satellites naturels en orbite. De nos jours, beaucoup de satellites artificiels sont en orbite autour de la Terre.
Les trois lois de Kepler permettent de déterminer par le calcul le mouvement orbital.
Éléments orbitaux
Une orbite elliptique peut se définir dans l'espace selon six paramètres permettant de calculer très précisément la trajectoire complète. Deux de ces paramètres (excentricité et demi-grand axe) définissent la trajectoire dans un plan, trois autres (inclinaison, longitude du nœud ascendant et argument du péricentre) définissent l'orientation du plan dans l'espace et le dernier (instant de passage au péricentre) définit la position de l'objet. Voici la description plus détaillée de ces paramètres :
- Demi-grand axe a : la moitié de la distance qui sépare le péricentre de l'apocentre (le plus grand diamètre de l'ellipse). Ce paramètre définit la taille absolue de l'orbite. Il n'a de sens en réalité que dans le cas d'une trajectoire elliptique ou circulaire (le demi-grand-axe est infini dans le cas d'une parabole ou d'une hyperbole)
- Excentricité e : une ellipse est le lieu des points dont la somme des distances à deux points fixes, les foyers (S et S' sur le diagramme), est constante. L'excentricité mesure le décalage des foyers par rapport au centre de l'ellipse (C sur le diagramme); c'est le rapport de la distance centre-foyer au demi-grand-axe. Le type de trajectoire dépend de l'excentricité :
- e = 0 : trajectoire circulaire
- 0 < e < 1 : trajectoire elliptique
- e = 1 : trajectoire parabolique
- e > 1 : trajectoire hyperbolique
- Inclinaison i : l'inclinaison (entre 0 et 180 degrés) est l'angle que fait le plan orbital avec un plan de référence. Ce dernier étant en général le plan de l'écliptique dans le cas d'orbites planétaires (plan contenant la trajectoire de la Terre; en noir dans la figure 1). L'inclinaison est l'angle orange dans la figure 1.
- Longitude du nœud ascendant ☊ : il s'agit de l'angle entre la direction du point vernal et la ligne des nœuds, dans le plan de l'écliptique. La direction du point vernal (en noir dans la figure 1) est la droite contenant le Soleil et le point vernal (point de repère astronomique correspondant à la position du Soleil au moment de l'équinoxe du printemps). La ligne des nœuds (en vert dans la figure 1) est la droite à laquelle appartiennent les nœuds ascendant (le point de l'orbite où l'objet passe du côté nord de l'écliptique) et descendant (le point de l'orbite où l'objet passe du côté sud de l'écliptique).
- Argument du périhélie ω: il s'agit de l'angle formé par la ligne des nœuds et la direction du périhélie (la droite à laquelle appartiennent le Soleil et le périhélie de la trajectoire de l'objet), dans le plan orbital. Il est en bleu dans la figure 1. La longitude du périhélie est la somme de la longitude du nœud ascendant et de l'argument du périhélie.
- Instant τ de passage au périhélie : La position de l'objet sur son orbite à un instant donné est nécessaire pour pouvoir la prédire pour tout autre instant. Il y a deux façons de donner ce paramètre. La première consiste à spécifier l'instant du passage au périhélie. La seconde consiste à spécifier l'anomalie moyenne M (en rouge dans la figure 1) de l'objet pour un instant conventionnel (l'époque de l'orbite). L'anomalie moyenne n'est pas un angle physique, mais spécifie la fraction de la surface de l'orbite balayée par la ligne joignant le foyer à l'objet depuis son dernier passage au périhélie, exprimée sous forme angulaire. Par exemple, si la ligne joignant le foyer à l'objet a parcouru le quart de la surface de l'orbite, l'anomalie moyenne est