Modèles de régression multiple postulés et non postulés - Définition

Modèle

Un modèle relie une ou plusieurs variables à expliquer Y à des variables explicatives X, par une relation fonctionnelle Y = F(X)

• Un modèle physique est un modèle explicatif soutenu par une théorie.
• Un modèle statistique, au contraire, est un modèle empirique issu de données disponibles, sans connaissance a priori sur les mécanismes en jeu. On peut cependant y intégrer des équations physiques (lors du pré traitement des données).

Modèle postulé

Dans le modèle précédent, seuls les coefficients sont « dirigés par les données », la structure polynomiale du modèle est imposée par l’utilisateur (selon son expertise du problème), qui postule a priori :

• le type de modèle : linéaire ou polynomial, et le degré du polynôme,
• les variables qui entreront dans le modèle.

Exemple de modèle polynomial avec deux variables explicatives :

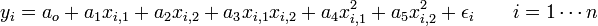
Régression multiple

C’est le plus utilisé des modèles statistiques.

On dispose de n observations (i = 1,…, n ) de p variables. L'équation de régression s'écrit

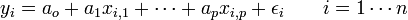
où

• ε_i est l'erreur du modèle;
• a₀, a₁, …, a_p sont les coefficients du modèle à estimer.

Le calcul des coefficients a_j et de l'erreur du modèle, à partir des observations, est un problème bien maîtrisé (voir la Régression linéaire multiple).

Plus délicat est le choix des variables entrant dans le modèle. Il peut être postulé ou non postulé.

Modèle non postulé

Le modèle « non postulé » est au contraire entièrement « dirigé par les données », aussi bien sa structure mathématique que ses coefficients.

La sélection des variables explicatives ne demande pas de connaissance a priori sur le modèle : elle a lieu parmi un ensemble très grand de variables, comprenant :

• les variables explicatives simples : A, B, C,... (proposées par les experts du domaine considéré et dont le nombre p peut être supérieur à n) ;
• des « interactions » ou « couplage » de ces variables, par exemple « A*B » (produit croisé sur variables centrées-réduites), mais aussi des « interactions logiques » tel « A et B », « A ou B », « A et B moyens », « A si B est fort », « A si B est moyen », « A si B est faible », etc. ;
• des fonctions de ces variables : par exemple cos(A) ou n’importe quelle fonction sinusoïdale amortie ou amplifiée, fonction périodique non sinusoïdale, effet de seuil, etc.

La sélection est faite avant le calcul des coefficients de la régression selon le principe suivant :

On cherche le facteur, ou l'« interaction », ou la fonction, le mieux corrélé à la réponse. L'ayant trouvé, on cherche le facteur, ou l'interaction, le mieux corrélé au résidu non expliqué par la corrélation précédente; etc. Cette méthode vise à ne pas compter deux fois la même influence, lorsque les facteurs sont corrélés, et à les ordonner par importance décroissante.

La liste trouvée, classée par ordre d’importance décroissante, ne peut pas compter plus de termes que d’inconnues (n). Si l’on ne garde qu’un terme dans le modèle, ce devra être le premier de la liste. Si l’on n’en garde que deux, ce seront les deux premiers, etc.

En effet, puisque chacun des termes de la liste "explique" le résidu non expliqué par les précédents, les derniers n'expliquent peut-être que du "bruit". Quel critère d'arrêt choisir ?

Le nombre de termes conservés dans le modèle peut être, par exemple, celui qui minimise l’erreur standard de prédiction SEP (Standard error of Prediction), ou celui qui maximise le F de Fisher. Ce nombre de terme peu aussi être choisi par l’utilisateur à partir de considérations physiques.

Exemple : on suppose que l’ensemble des « variables explicatives » candidates est {A,B,C,D,E,F,G}, et que le modèle obtenu est :

Y = constante + a.A + b.(« E et G ») + c.(« D et F moyens »)

On remarque que

* les variables B et C, non pertinentes, ne figurent pas dans le modèle

* la variable A est apparue comme terme simple,

* les variables E et G d’une part, et D et F, d’autre part, n’apparaissent que comme « interactions logiques ».

Ce modèle « parcimonieux »,c'est-à-dire comportant peu de termes (ici trois), fait intervenir 5 variables, et collera mieux à la réalité physique qu’un modèle polynomial. En effet la conjonction « E et G » qui signifie « E et G forts simultanément » est plus souvent rencontrée dans la réalité physique (exemple : la catalyse en chimie) qu'un terme polynomial de type E.G.