Module semi-simple - Définition

Exemples

Espace vectoriel des endomorphismes

L'exemple historique qui a amené à étudier les premières études sur ce qui est devenu plus tard la définition des modules semi-simples correspond à des modules correspondant à des idéaux de l'espace des endomorphismes. Supposons le corps K commutatif et algébriquement clos, et V un espace vectoriel de dimension finie sur K. Si L(V) désigne l'espace vectoriel des endomorphismes, alors une sous-algèbre M de L(V) est un module sur l'anneau M. Il existe un résultat important concernant ce type de module :

• Soit φ un endomorphisme de L(V), la sous-algèbre engendrée par φ est un module sur lui-même. Il est semi-simple si et seulement si le polynôme minimal de φ n'admet pas de racine multiple.

Ce résultat est l'application directe de la réduction de Jordan, si le polynôme minimal de φ n'a pas de racine multiple, alors l'algèbre engendrée par φ est composée d'une somme directe des homothéties dans chaque sous-espace propre. Si m désigne le nombre de sous-espace propre, le module est isomorphe à K^m. Dans le cas contraire, il existe une composante nilpotente qui rend un sous-espace caractéristique non semi-simple.

Structure de G-module

Un exemple qui a largement fait évoluer la théorie est celui des G-modules ou G désigne un groupe. L'anneau associée correspond à la structure d'algèbre sur un corps K commutatif des combinaisons linéaires formelles des éléments de G :

• La K-algèbre du groupe G, noté K[G] est l'espace vectoriel des combinaisons linéaires formelles des éléments de G et muni de la multiplication suivante :

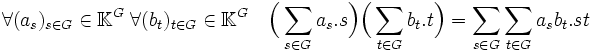
Soit (V, ρ) une représentation, la fonction ρ se prolonge sur K[G] de la manière suivante :

Le théorème de Maschke montre que sous G-module est un facteur direct, en conséquence un un G-module est un module semi-simple.