Réduction de Jordan - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La réduction de Jordan est la traduction matricielle de la réduction des endomorphismes introduite par Jordan. Cette réduction est tellement employée, en particulier en analyse pour la résolution d'équations différentielles ou pour déterminer le terme général de suites récurrentes, qu'on la nomme parfois « jordanisation des endomorphismes ».
Elle consiste à exprimer la matrice d'un endomorphisme dans une base où l'expression de l'endomorphisme est réduite, dite base de Jordan. La réduction consiste à déterminer une décomposition de Dunford c'est-à-dire trouver un endomorphisme diagonalisable et un endomorphisme nilpotent tel que les deux commutent et que leur somme soit égale à l'endomorphisme initial, puis sur chaque espace caractéristique on effectue une réduction de Jordan. Cette dernière est un cas particulier de la décomposition de Frobenius dans la cadre spécifique d'un endomorphisme nilpotent.
Construction de la base de Jordan
Soit u un endomorphisme sur un espace vectoriel E tel que son polynôme minimal soit scindé. Il possède alors les propriétés suivantes:
-
- E est la somme directe des espaces caractéristiques de u. Ils sont notés ici Ei et les valeurs propres associés λi.
-
- La restriction de u à Ei est la somme d'une homothétie de rapport λi et d'un endomorphisme nilpotent noté ni.
Ces résultats sont démontrés dans l'article décomposition de Dunford.
-
- Il existe une base Eij de Ei
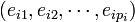
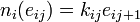
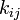
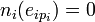
- Il existe une base Eij de Ei
Ce résultat est démontré dans l'article Endomorphisme nilpotent.
Jordanisation d'un endomorphisme dans un corps algébriquement clos
On considère un endomorphisme dans un espace vectoriel de dimension finie, de polynôme caractéristique scindé. Le théorème de Jordan nous informe qu'il admet une représentation matricielle de la forme suivante
où les scalaires λi sont les valeurs propres de l'endomorphisme considéré.
Ainsi sur un corps algébriquement clos, et par exemple dans

Attention : il n'y a pas a priori un bloc de Jordan pour chaque valeur propre, plusieurs λi peuvent avoir la même valeur.
Propriétés des blocs
Prenons un endomorphisme u admettant une telle représentation. On étudie une valeur propre particulière λ de l'endomorphisme u. On regroupe ensemble les vecteurs associés aux blocs
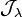
- La multiplicité de λ (multiplicité dans le polynôme caractéristique) est égale à la dimension de l'espace caractéristique.
- La multiplicité de λ dans le polynôme minimal est égal à l'indice de nilpotence de l'endomorphisme nλ.
Application aux classes de similitude des matrices
On se place sur un corps algébriquement clos. Deux matrices sont semblables si et seulement si elles ont la même écriture en blocs de Jordan, à l'ordre près des blocs.
Blocs de Jordan
On appelle bloc de Jordan une matrice de la forme

On appelle bloc de Jordan nilpotent une telle matrice où les coefficients diagonaux sont tous nuls, c'est-à-dire de la forme

Réduction de Jordan et systèmes différentiels
Un système d'équations différentielles linéaires en y peut se réduire à une équation différentielle matricielle d'ordre 1 : u'(t) = Au(t) et la condition initiale u(0) = u0, où u(t) est un vecteur colonne contenant les dériviées successives de y. La résolution est alors explicite lorsque le système d'équations différentielles est à coefficients constants : u(t) = exp(tA)u0. L'avantage de la forme normale de Jordan réside dans la facilité de calculs des matrices des blocs de Jordan. En effet, l'exponentielle d'un bloc de Jordan nilpotent de taille p est
On voit de cette manière l'intérêt calculatoire de cette méthode.



















































