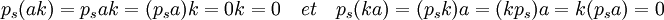Théorème de Maschke - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et plus précisément en algèbre, le théorème de Maschke est un des théorèmes fondamentaux de la théorie de la représentation des groupes.
Ce théorème permet, si la caractéristique du corps est soit nulle soit première avec l'ordre du groupe, d'établir une décomposition de la représentation en facteurs irréductibles. Elle admet des généralisations pour l'étude des G-modules, des algèbres de groupes et des groupes de Lie.
Ce théorème doit son nom au mathématicien Heinrich Maschke .
Énoncés des théorèmes
Le cas le plus simple est celui de la représentation d'un groupe fini :
-
- Soit (V, ρ) une représentation d'un groupe G d'ordre fini sur un corps K de caractéristique nulle ou première avec l'ordre de G, alors V est somme directe de sous-espaces irréductibles.
En terme matriciel, cela signifie qu'il existe une unique décomposition optimale, en somme de sous-espaces vectoriels, de l'espace vectoriel V, telle que tous les automorphismes de la représentation s'écrivent sous forme diagonale par blocs suivant cette décomposition ; l'optimalité étant choisie dans le sens qu'aucune décomposition plus fine ne conserverait la propriété d'écriture diagonale par blocs des automorphismes considérés.
Cette définition est équivalente à la donnée d'un G-module :
-
- Soit V un G-module sur un groupe G d'ordre fini sur un corps K de caractéristique nulle ou première avec l'ordre de G, alors V est semi-simple.
Ce théorème possède une expression analogue en termes d'algèbre d'un groupe fini :
-
- Si K est un corps de caractéristique nulle ou première avec l'ordre de G un groupe fini, alors l'algèbre de groupe K[G] est semi-simple.
Ce théorème possède une généralisation. Si le groupe est topologique, il peut parfois être muni d'une mesure compatible avec la loi du groupe et appelée mesure de Haar. C'est le cas par exemple des groupes compacts. Les conséquences du théorème sont alors encore vérifiées.
Un lemme est utile pour établir le résultat :
-
- Si W est un sous-espace vectoriel stable de la représentation, alors il existe un sous-espace supplémentaire de W stable pour la représentation.
En effet, notons Wq un supplémentaire quelconque de W et p le projecteur sur W parallèlement à Wq. Considérons alors l'application linéaire ps définie par :
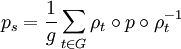
Où g désigne l'ordre du groupe G.
Montrons que ps est un projecteur. La restriction de ps à W est égale à l'identité, car la restriction de p à W est égale à l'identité et que ρt laisse W stable. De plus, l'image de ps est égale à W.
Montrons que, si Ws est le noyau de ps, alors il est stable par la représentation. Remarquons tous d'abord que si u est un élément du groupe, l'application de G dans G, qui à t associe ut est une permutation. En conséquence :
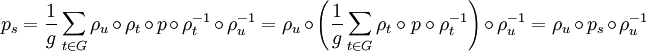
Soit k un élément du noyau, montrons alors que ρu(k) est aussi élément du noyau.
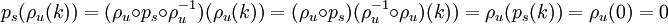
Ws est un supplémentaire de W car c'est le noyau d'un projecteur sur W et il est stable par la représentation, le lemme est donc démontré.
-
- Soit (V, ρ) une représentation d'un groupe G d'ordre fini sur un corps K de caractéristique nulle ou première avec l'ordre de G, alors V est somme directe de sous-espaces irréductibles.
- Si n est égal à un, alors il n'existe aucun sous-espace vectoriel stable non trivial, donc le théorème est manifestement vérifié.
- Supposons le théorème vrai pour toute dimension strictement inférieure à n. Si la représentation est irréductible, alors le théorème est vérifié. Dans le cas contraire il existe un sous-espace stable W de dimension strictement inférieur à n. Le lemme garantit l'existence d'un supplémentaire Ws stable, aussi de dimension strictement inférieur à n. Par hypothèse de récurrence, W et Ws sont sommes directes de sous-espaces stables par la représentation. Le fait que W et Ws soient des supplémentaires permet de conclure. Cette démonstration s'applique de la même manière aux G-modules.
-
- Si K est un corps de caractéristique nulle ou première avec l'ordre de G un groupe fini, alors l'algèbre de groupe K[G] est semi-simple.
L'objectif est maintenant de montrer que le noyau de ps est un idéal bilatère. La théorie des anneaux permet de conclure, c'est un idéal nommé idéal annulateur. Démontrons le dans ce contexte. Soit a un élément de l'idéal annulateur et k un élément quelconque de K[G]. L'objectif est de montrer que ps(ak) = ps (ka) = 0. Il suffit de remarque de ps commutent avec tous les éléments de K[G] car il commute sur une base.