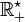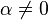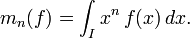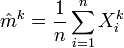Moment (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En probabilités (mathématiques, statistiques), on définit le moment d'ordre n>0 d'une variable aléatoire X, s'il existe, le nombre
![m_n = \mathbb{E}[~X^n~] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/956669df6cd728c9c1b239118a6d810f_a0a62ac97f645087ad8bcbd9b9a2aa65.png)
Notion de moment
La notion de moment en mathématiques, notamment en calcul des probabilités, a pour origine la notion de moment en physique.
Soit une fonction
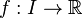
Remarque : pour un entier naturel n donné, l'ensemble des fonctions continues sur I dont le moment d'ordre n existe est un espace vectoriel réel, et l'application
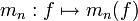
Moments centrés
On définit le moment centré d'ordre n>0 d'une variable aléatoire X, s'il existe, le nombre
![\mu_n = \mathbb{E}[~(X-\mathbb{E}(X))^n~] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0d94866db25ef4b877bf490c923f5e20_b92fb8eaadbbe18473f791d13b52ced7.png)
Estimation des moments
Lorsque le moment existe, on utilise souvent l'estimateur suivant pour le moment d'ordre k:
à partir de l'échantillon
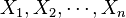
On peut montrer que cet estimateur est sans biais.
Formules de détermination récursive des moments
En définissant
- Les moments par rapport à l'origine (moments ordinaires ou raw moments en anglais):
![m_k(X) \equiv \mathbb{E}\left[X^k\right]\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/80d485727e1e76b12d729ab9673c42b5_a7e24d7e2ab29d412ef89e4b4acdb270.png)
.
- Les moments centrés, notés généralement
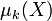
![\mu_k(X) \equiv \mathbb{E}[(X-\mathbb{E}[X])^k]\,](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b24b53eb0e628ea13b82261466e8ca2b_dc730bf4e5ca0e447c30c1232d12b917.png)
Il existe des formules (qui ressemblent à celle du binôme) permettant de calculer un moment centré d'ordre k à partir des moments ordinaires d'ordre inférieur ou égal à k, et réciproquement ; voici quelques exemples (jusqu'à l'ordre 4) :
-
-
-
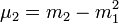
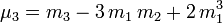
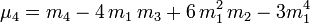
- et :
-
-
-
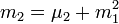
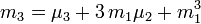
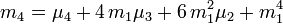
Moments remarquables
Certains moments sont connus sous un nom particulier. Ils sont utilisés couramment pour caractériser une variable aléatoire.
- Le moment d'ordre un de la variable :
![m_1 = \mathbb{E}[X] \,](https://static.techno-science.net/illustration/Definitions/autres/b/bd52ef95ef0ed57eb37974699f17dfe9_3b783a0fee067183785a93ed00f3bcf0.png)
![m_1 = \mathbb{E}[X] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/bd52ef95ef0ed57eb37974699f17dfe9_3b783a0fee067183785a93ed00f3bcf0.png)
- Le moment d'ordre deux de la variable centrée :
![\mu_2 = \sigma^2 = \mathbb{E} \left [\left(X-\mu\right)^2\right] \,](https://static.techno-science.net/illustration/Definitions/autres/7/74c6f9d94f20fa7198c50228e3ba9db4_441b42e8922858e39bd73617cc919715.png)
![\mu_2 = \sigma^2 = \mathbb{E} \left [\left(X-\mu\right)^2\right] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/74c6f9d94f20fa7198c50228e3ba9db4_441b42e8922858e39bd73617cc919715.png)
- Le moment d'ordre trois de la variable centrée-réduite :
![\gamma_1 = \frac {\mu_3} {\sigma^3} = \mathbb{E} \left[ \left(\frac{X-\mu}{\sigma} \right)^3 \right] \,](https://static.techno-science.net/illustration/Definitions/autres/c/c9406aeaf9d57d3545dabedba2db6715_d1231b899f97fcca1617b7d10d2a0396.png)
![\gamma_1 = \frac {\mu_3} {\sigma^3} = \mathbb{E} \left[ \left(\frac{X-\mu}{\sigma} \right)^3 \right] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/c/c9406aeaf9d57d3545dabedba2db6715_d1231b899f97fcca1617b7d10d2a0396.png)
- Le moment d'ordre quatre de la variable centrée-réduite :
![\beta_2 = \frac{\mu_4} {\sigma^4} = \mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right] \,](https://static.techno-science.net/illustration/Definitions/autres/d/dc437855595cc90f82e3f0660e702725_f95fb5277a1904a634ac7f5057e85f62.png)
![\beta_2 = \frac{\mu_4} {\sigma^4} = \mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/dc437855595cc90f82e3f0660e702725_f95fb5277a1904a634ac7f5057e85f62.png)
Problème des moments
On peut se demander si une fonction continue
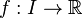
En d'autres termes : soient deux fonctions continues
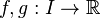
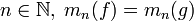
- D'après un théorème de Hausdorff, la réponse est affirmative lorsque I est un segment
![[a,\, b]](https://static.techno-science.net/illustration/Definitions/autres/d/d2524b9940ce1c636bfb26ae09a941d2_de57359067f6b3298050b33ed863e8df.png)
La fonction h = f − g est continue sur I, et tous ses moments sont nuls, car pour tout n, mn(h) = mn(f) − mn(g).
On en déduit, par linéarité de l'intégrale, que
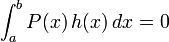
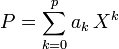
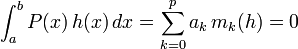
Or, d'après un théorème de Weierstrass, pour toute fonction continue
![[a,\, b] \to \R](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8cc3f85cff4e3a1bba2863994946dad1_d90789c7bd1609fea1eb2f764e3379e9.png)
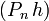
![[a,\, b]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d2524b9940ce1c636bfb26ae09a941d2_de57359067f6b3298050b33ed863e8df.png)
![\int_a^b [h(x)]^2\,dx = \lim_{n \to +\infty} \int_a^b P_n(x)\,h(x)\,dx = 0](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/6d0d4bf8aaa69019e42e375be04dd86c_cfc0d0c490e59cc28b07ec2ff5c54061.png)
Comme h est continue sur le segment
- Dans le cas général, la réponse est négative. Voici un contre-exemple probabiliste donné par William Feller. On considère la fonction
![f :\, ]0,\, +\infty[\, \to \R^+](https://static.techno-science.net/illustration/Definitions/autres/d/d18e5037d82a35ba5c710196f746ae64_3b353641188cdbb425a72fd4870f77de.png)
![f :\, ]0,\, +\infty[\, \to \R^+](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d18e5037d82a35ba5c710196f746ae64_3b353641188cdbb425a72fd4870f77de.png)
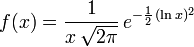
- On démontre (par changement de variable) que pour tout entier naturel n,
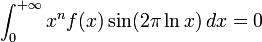
- Pour tout
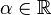
![g_\alpha :\, ]0,\, +\infty[\, \to \R](https://static.techno-science.net/illustration/Definitions/autres/f/fc6469176b50c8c637c7f4cb9022141c_d3428849913b2280882196c314c32afa.png)
![g_\alpha(x) = f(x)\, [1 + \alpha \sin(2 \pi \ln x)]](https://static.techno-science.net/illustration/Definitions/autres/4/444a99c9e089466f8f18db4e8200403f_6c5ddf0708af64ed2836259e306c1747.png)
![g_\alpha :\, ]0,\, +\infty[\, \to \R](https://static.techno-science.net/illustrationWebp/Definitions/autres/f/fc6469176b50c8c637c7f4cb9022141c_d3428849913b2280882196c314c32afa.png)
![g_\alpha(x) = f(x)\, [1 + \alpha \sin(2 \pi \ln x)]](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/444a99c9e089466f8f18db4e8200403f_6c5ddf0708af64ed2836259e306c1747.png)
- Alors : quels que soient
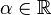
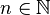
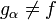
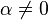
- Nota : pour tout
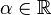
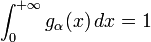
![\alpha \in [-1,\, +1]](https://static.techno-science.net/illustration/Definitions/autres/9/9f09b2ad785cc12d642d764d48b337a7_368b38de874db5013a8481fe8f8e3742.png)
![\alpha \in [-1,\, +1]](https://static.techno-science.net/illustrationWebp/Definitions/autres/9/9f09b2ad785cc12d642d764d48b337a7_368b38de874db5013a8481fe8f8e3742.png)
