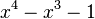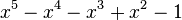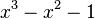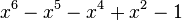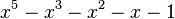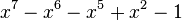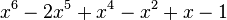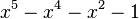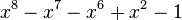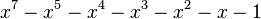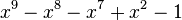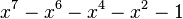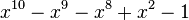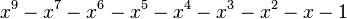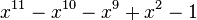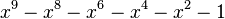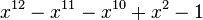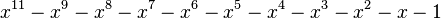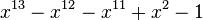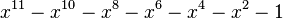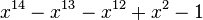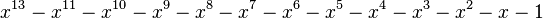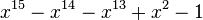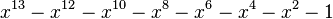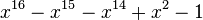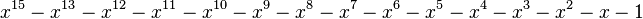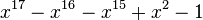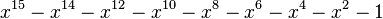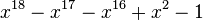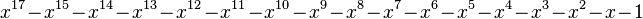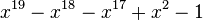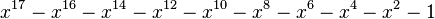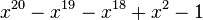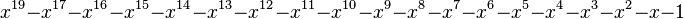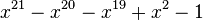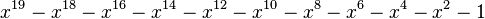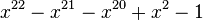Nombre de Pisot-Vijayaraghavan - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Table des nombres de Pisot

Introduction

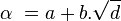
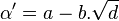
En mathématiques, un nombre de Pisot-Vijayaraghavan est un entier algébrique réel strictement supérieur à 1, dont tous les éléments conjugués ont un module strictement inférieur à 1. Par exemple, le nombre entier quadratique $\alpha\ = a + b.\sqrt d\,$ , où a et b sont tous deux des entiers ou la moitié d'un entier impair, admet un conjugué $\alpha' = a - b.\sqrt d\,$ ; les conditions sont alors :

$\alpha > 1\,$ et

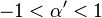
Ces conditions sont satisfaites par le nombre d'or $\varphi\,$ . Nous avons alors :

$\varphi = \frac{(1 + \sqrt5)}{2} > 1\,$

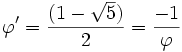
La condition générale fut étudiée par G. H. Hardy en relation avec un problème d'approximation diophantienne. Ce travail fut rejoint par Tirukkannapuram Vijayaraghavan (30 novembre1902 - 20 avril 1955), un mathématicien indien de la région de Madras qui vint à Oxford pour travailler avec Hardy dans le milieu des années 1920. La même condition apparaît aussi dans certains problèmes sur les séries de Fourier et fut étudiée plus tard par Charles Pisot. Le nom, formé par ces deux auteurs, est maintenant communément en usage.

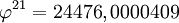
Les nombres de Pisot-Vijayaraghavan peuvent être utilisés pour engendrer presque tous les entiers : la nième puissance d'un nombre de Pisot "approche les entiers" quand n tend vers l'infini. Par exemple, $\varphi^{21} = 24476,0000409$ . L'effet peut même être plus prononcé pour les nombres de Pisot-Vijayaraghavan engendrés à partir d'équations de degré plus élevé.

Cette propriété provient du fait que pour chaque n, la somme des n-ièmes puissances d'un entier algébrique x et de ses conjugués est exactement un entier ; lorsque x est un nombre de Pisot, les n-ièmes puissances des (autres) conjugués tendent vers 0 quand n tend vers l'infini.

Le plus petit nombre de Pisot-Vijayaraghavan est l'unique racine réelle du polynôme $x^3 - x - 1\,$ , connu sous le nom de nombre plastique ou nombre d'argent (approximativement 1,324718).

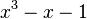
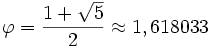
Le plus petit point d'accumulation de l'ensemble des nombres de Pisot-Vijayaraghavan est le nombre d'or $\varphi = \frac{1 + \sqrt 5}{2} \approx 1,618033$ .

	Valeur	Racine de...
1	1,3247179572447460260	$x^3-x-1\,$
2	1,3802775690976141157	$x^4-x^3-1\,$
3	1,4432687912703731076	$x^5-x^4-x^3+x^2-1\,$
4	1,4655712318767680267	$x^3-x^2-1\,$
5	1,5015948035390873664	$x^6-x^5-x^4+x^2-1\,$
6	1,5341577449142669154	$x^5-x^3-x^2-x-1\,$
7	1,5452156497327552432	$x^7-x^6-x^5+x^2-1\,$
8	1,5617520677202972947	$x^6-2x^5+x^4-x^2+x-1\,$
9	1,5701473121960543629	$x^5-x^4-x^2-1\,$
10	1,5736789683935169887	$x^8-x^7-x^6+x^2-1\,$
11	1,5900053739013639252	$x^7-x^5-x^4-x^3-x^2-x-1\,$
12	1,5911843056671025063	$x^9-x^8-x^7+x^2-1\,$
13	1,6013473337876367242	$x^7-x^6-x^4-x^2-1\,$
14	1,6017558616969832557	$x^{10}-x^9-x^8+x^2-1\,$
15	1,6079827279282011499	$x^9-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
16	1,6081283851873869594	$x^{11}-x^{10}-x^9+x^2-1\,$
17	1,6119303965641198198	$x^9-x^8-x^6-x^4-x^2-1\,$
18	1,6119834212464921559	$x^{12}-x^{11}-x^{10}+x^2-1\,$
19	1,6143068232571485146	$x^{11}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
20	1,6143264149391271041	$x^{13}-x^{12}-x^{11}+x^2-1\,$
21	1,6157492027552106107	$x^{11}-x^{10}-x^8-x^6-x^4-x^2-1\,$
22	1,6157565175408433755	$x^{14}-x^{13}-x^{12}+x^2-1\,$
23	1,6166296843945727036	$x^{13}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
24	1,6166324353879050082	$x^{15}-x^{14}-x^{13}+x^2-1\,$
25	1,6171692963550925635	$x^{13}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
26	1,6171703361720168476	$x^{16}-x^{15}-x^{14}+x^2-1\,$
27	1,6175009054313240144	$x^{15}-x^{13}-x^{12}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
28	1,6175012998129095573	$x^{17}-x^{16}-x^{15}+x^2-1\,$
29	1,6177050699575566445	$x^{15}-x^{14}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
30	1,6177052198884550971	$x^{18}-x^{17}-x^{16}+x^2-1\,$
31	1,6178309287889738637	$x^{17}-x^{15}-x^{14}-x^{13}-x^{12}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
32	1,6178309858778122988	$x^{19}-x^{18}-x^{17}+x^2-1\,$
33	1,6179085817671650120	$x^{17}-x^{16}-x^{14}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
34	1,6179086035278053858	$x^{20}-x^{19}-x^{18}+x^2-1\,$
35	1,6179565199535642392	$x^{19}-x^{17}-x^{16}-x^{15}-x^{14}-x^{13}-x^{12}-x^{11}-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x-1\,$
36	1,6179565282539765702	$x^{21}-x^{20}-x^{19}+x^2-1\,$
37	1,6179861253852491516	$x^{19}-x^{18}-x^{16}-x^{14}-x^{12}-x^{10}-x^8-x^6-x^4-x^2-1\,$
38	1,6179861285528618287	$x^{22}-x^{21}-x^{20}+x^2-1\,$