Nombre et supernombre de Poulet - Définition
La liste des auteurs de cet article est disponible ici.
Nombres de Poulet à deux facteurs premiers
On l'a vu, les nombres de Poulet à deux facteurs premiers sont des supernombres de Poulet.
On peut également les caractériser comme suit : Soient p et q deux nombres premiers ; leur produit pq est un nombre de Poulet si, et seulement si, q divide 2p - 2 et p divise 2q - 2.
Reformulons le résultat avec le formalisme de l'arithmétique modulaire :
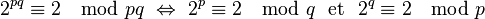
Rappelons que le petit théorème de Fermat assure que


On a donc
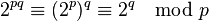
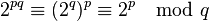
D'autre part, p et q étant premiers, par une application simple du théorème des restes chinois, on a l'équivalence suivante :
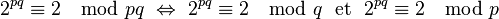
Liens externes et sources
Sur l'encyclopédie électronique des suites entières de Sloane on trouve :
- La suite A001567 des nombres de Poulet
- La suite A050217 des supernombres de Poulet
- La suite A006935 des nombres de Poulet pairs
Cette page (en anglais) donne beaucoup d'informations sur les nombres et supernombres de Poulet :
- Pseudoprimes (Gérard Michon)
Nombres de Poulet pairs
On connait des nombres de Poulet pairs ; le plus petit d'entre eux, 161038 = 2 × 73 × 1103, a été découvert par Derrick Lehmer en 1950.
Il est par ailleurs assez facile de démontrer qu'il n'y a pas de supernombres de Poulet pairs. En effet, un tel nombre admettrait un diviseur composé de la forme 2p avec p premier, qui serait un nombre de Poulet. Or
Si c'est un nombre de Poulet, il est divisible par 2p: on en déduit que
p divise (2p − 2)(2p − 1 + 1) + 1.
Or, d'après le petit théorème de Fermat, p divise (2p − 2). On a alors p divise 1, ce qui est absurde. Il n'existe donc pas de nombre de Poulet de la forme 2p avec p premier, et a fortiori pas de supernombre de Poulet pair.

















































