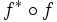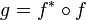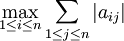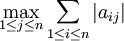Norme d'opérateur - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Norme duale
Dans le cas où
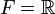
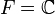
Norme d'un endomorphisme
Dans le cas où E=F, on choisit usuellement (même si ce n'est pas obligatoire)
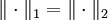
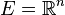
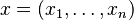

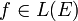
- Si
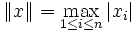
- Si
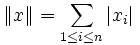
- Si