Dual topologique - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Définition - Dual topologique d'un espace de Hilbert - Topologies duales - Bidual (topologique)

Définition

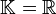
Soit $\mathbb E$ un espace vectoriel topologique sur le corps $\mathbb K = \mathbb R$ ou $\mathbb C$ .

Le dual topologique $\mathbb {E'}$ de $\mathbb E$ est le sous-espace de $\mathbb{E} ^*$ (espace dual de E) formé des formes linéaires continues (il est immédiat que c'est bien un sous-espace vectoriel).

Si l'espace est de dimension finie le dual topologique coïncide avec le dual (algébrique) puisque dans ce cas toute forme linéaire est continue.

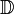
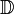
Par contre ceci est inexact dans le cas général. Ainsi par exemple envisageons l'espace vectoriel réel $\mathbb D$ des fonctions dérivables de l'intervalle $[0,1]$ dans $\mathbb R$ muni de la topologie de la norme uniforme $n(f)=\sup_{x \in [0,1]}|f(x)|$ . Soit alors $\quad p$ la forme linéaire définie par $\quad p(f)=f'(0)$ . Soit par ailleurs la suite $\quad (f_n)_{n>0}$ de fonctions de $\mathbb D$ définie par $\quad f_n(x)=x(1-x)^n$ . On constate facilement que $\lim_{n \to\infty}f_n=0$ (la fonction $\quad f_n$ est positive et maximale pour $\quad x=1/(n+1)$ ). Mais $\quad p(f_n)=1$ pour tout $n$ alors que $\quad p(f_n)$ devrait tendre vers $\quad p(0)=0$ si $\quad p$ était continue !

Dual topologique d'un espace de Hilbert

Nous allons prouver le résultat fondamental suivant :

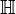
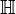
Le dual topologique $\mathbb {H'}$ d'un espace de Hilbert $\mathbb H$ est l'image de $\mathbb H$ par l'isomorphisme $\quad j$ tel que l'image $\quad j(v)$ d'un vecteur $\quad v \in \mathbb H$ soit la forme linéaire définie par $\forall w \in \mathbb H, \langle j(v),w\rangle=(v|w)$ (produit scalaire).

En effet, l'application $\quad j(v)$ est clairement une forme linéaire (« en $w$ »), continue en vertu de l'inégalité de Cauchy-Schwarz.

$\quad j$ est évidemment linéaire.

Si $\quad j(v)=0$ , quel que soit $\quad w \in \mathbb H$ , $\quad(v|w)=0$ . En appliquant ceci à $\quad w=v$ on déduit $\quad v=0$ , ce qui montre que $\quad j$ est injective.

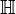
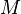
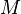
Montrons enfin que $\quad j$ est surjective. Tout d'abord $\quad j(0)=0$ . Soit à présent $\quad p$ une forme linéaire non nulle continue sur $\mathbb H$ . L'hyperplan vectoriel $\quad M$ d'équation $\quad p(v)=0$ est fermé. La théorie de la projection sur un hyperplan fermé d'un Hilbert (cf. espace de Hilbert) montre l'existence d'un vecteur unitaire $u$ orthogonal à cet hyperplan $\quad M$ et de plus $\quad H=M \oplus vect(u)$ . 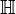Tout vecteur w de $\mathbb H$ s'écrit de manière unique $\quad w=(u|w)u+w'$ avec $\quad w' \in M$ . Il en résulte que $\quad p(w)=(u|w)p(u)=(p(u)u|w)$ puisque $\quad p(w')=0$ . Ainsi $\quad j(p(u)u)=p$ .

Topologies duales

Nous allons dire quelques mots sur les topologies que l'on peut définir canoniquement dans certains cas sur le dual.

Topologie faible du dual

À tout vecteur v de $\mathbb E$ on peut faire correspondre l'application $\quad \nu _v$ de $\mathbb {E'}$ dans $\mathbb R$ définie par $\quad \nu_v(p)=|p(v)|$ .

Il est immédiat que $ν v$ est une semi-norme sur $\mathbb {E'}$ . On considère une famille finie J de semi-normes. On définit la semi-norme $p_J(x) = \sup_{i \in J}\ p_i(x)$ . Cette famille de semi-normes $p J$ est filtrante. La topologie définie par cette famille de semi-normes s'appelle topologie faible du dual. Muni de cette topologie, $\mathbb {E'}$ est un espace localement convexe. Comme conséquence du théorème de Hahn-Banach, la topologie définie ci-dessus est séparée.

Topologie forte sur le dual d'un espace normé

Si $\mathbb E$ est un espace vectoriel normé, on peut définir une norme duale $\| . \|'$ sur $\mathbb{E'}$ par

$\mathbb {E'}$ muni de cette norme (on dit "le dual fort") est un espace de Banach.

En effet soit $\quad p_n$ une suite de Cauchy de $\mathbb {E'}$ .

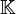
Pour tout $v \in \mathbb E$ la suite $\quad p_n(v)$ est une suite de Cauchy de $\mathbb K$ ( puisque $\quad |p_m(v)-p_n(v)|\le \|p_m-p_n\| \|v\|$ ). Il en résulte la définition d'une fonction $\quad p$ de $\mathbb E'$ dans $\quad K$ définie par $\quad p(v)=\lim_{n \to \infty}p_n(v)$ .

est une forme linéaire (algébrique): démonstration immédiate ("passage à la limite")

est continue:

et comme toute suite de Cauchy est bornée, il existe $\quad \lambda >0$ tel que

pour tout

. D'où

, ce qui montre que p est continue en 0 et donc continue sur

Le théorème de Banach-Alaoglu-Bourbaki affirme que la boule unité de l'espace dual d'un espace de Banach, muni de la norme de la topologie forte, est *-faiblement compacte.

Bidual (topologique)

Alors que la notion purement algébrique du bidual ne présente aucune ambiguïté, il en est tout autrement pour les notions topologiques. En effet selon la topologie retenue sur le dual les formes linéaires sur ce dual pourront être ou non continues.

Bidual d'un espace de Banach et réflexivité

Dans le cas d'un espace de Banach E, on qualifie en général de bidual le dual du dual muni de la topologie forte, noté $E''$ .

Il existe une application naturelle de E dans son bidual, l'application d'évaluation

qui constitue une injection isométrique. Lorsque J est une bijection, l'espace E est dit réflexif.

Par exemple, pour $1 < p < \infty$ , l'espace $l p$ des suites $(x n)$ telles que $\sum_{n=0}^\infty \left| x_n \right|^p$ converge, est réflexif. Son dual est l'espace des suites $(y n)$ telles que $\sum_{n=0}^\infty \left| y_n \right|^q$ converge, avec ${1 \over p} + {1 \over q}=1$ .

Par contre, l'espace $c 0$ des suites de limite nulle n'est pas réflexif. Son dual est l'espace $l 1$ des suites $(x n)$ telles que $\sum_{n=0}^\infty \left| x_n \right|$ converge, et dont le dual est $l^\infty$ , espace des suites bornées.

- Définition - Dual topologique d'un espace de Hilbert - Topologies duales - Bidual (topologique)

Des particules de lumière "filmés" dans leur déplacement 🎬

Montre moi tes mains, je te dirai quel buveur d'alcool tu es 🍺

Ces papillons interprètent les "cris" des plantes pour choisir où pondre 🦋

Le nombre d'articles scientifiques rétractés est en hausse ❌

Une nouvelle manière de lire les mémoires magnétiques 🧲

Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️

Ce nouveau modèle relie matière noire et inflation cosmique 🌀

Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡

Des mouches dans la station spatiale chinoise Tiangong 🛰️

Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️

Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟

Cette astuce simple réduit la consommation d'alcool... des femmes 🍷

Découverte: la lumière transforme un isolant en métal 💡

Cet aliment à bannir nourrit les cancers 🍽️

Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️

Découverte d'une chimie des océans refroidissant le climat 🌊

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Page générée en 0.219 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise