Norme (mathématiques) - Définition

Norme d'algèbre

Définition

Une norme sur une algèbre A est dite norme d'algèbre s'il existe une constante réelle C telle que

.

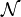
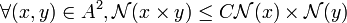
Quitte à multiplier la norme par C, cette constante peut être ramenée à 1. La condition est alors celle de sous-multiplicativité.

Dans le cas d'une algèbre réelle ou complexe, la condition est équivalente à la continuité du produit comme application bilinéaire.

Si l'algèbre est unitaire, on peut exiger de la norme qu'elle vérifie aussi :

,

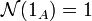
auquel cas la multiplication par une constante ne peut plus être utilisée pour « renormaliser » la norme.

Exemples

• L'application module est une norme d'algèbre sur considéré comme -algèbre.
• La norme d'opérateur sur est une norme d'algèbre.
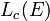
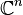
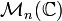
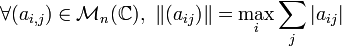
• La norme « infini » sur induit la norme d'opérateur sur qui s'écrit

.