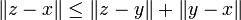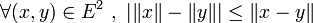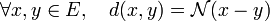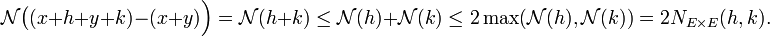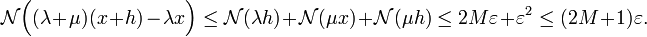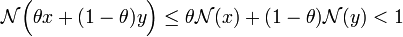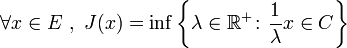Norme (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Sur un espace vectoriel quelconque
Définition formelle
Soit K un corps muni d'une valeur absolue et E un K-espace vectoriel.
Une norme sur E est une application
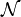
- séparation :
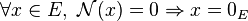
- homogénéité :
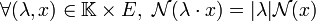
- sous-additivité (appelé également Inégalité triangulaire) :
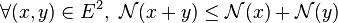
- Remarques
- Les corps des réels et des complexes ne sont pas les seuls à admettre une valeur absolue. Tout corps supporte la valeur absolue constante égale à 1 en dehors de 0.
Dans le cas des corps valués, la norme est même ultramétrique en vérifiant une certaine condition plus forte que la sous-additivité. - Une fonction de E dans
Un espace vectoriel muni d'une norme est alors appelé espace vectoriel normé (parfois abrégé en EVN).
L'image d'un vecteur x par la norme se note usuellement
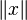
Premières propriétés
- La norme est sous-linéaire, c'est-à-dire qu'elle vérifie la propriété suivante :
-
-
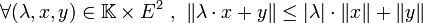
-
- Plus généralement, on obtient par récurrence immédiate l'inégalité dans

-
-
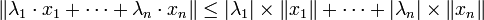
-
- La séparation et l'homogénéité garantissent les propriétés de séparation et de symétrie de la fonction
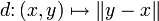
-
-
- nécessaire pour montrer que d est une distance sur E, qui plus est invariante par translation.
- Un espace vectoriel normé est donc un espace métrique homogène et la topologie associée est compatible avec les opérations vectorielles.
- La sous-additivité permet d'obtenir la propriété suivante :
-
-
- qui montre que la norme est une application 1-lipschitzienne donc continue.
- La norme est aussi une fonction convexe, ce qui peut être utile pour résoudre des problèmes d'optimisation.
Topologie
Une norme
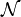
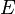
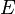
De plus, à d est associée, comme à toute distance, une topologie séparée. Un ouvert pour cette topologie est une partie
Cette topologie possède la propriété suivante :
Proposition — L'addition de
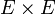
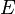
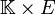
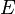
Soient
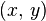
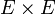
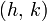
La majoration précédente montre que l'addition est 2-Lipschitzienne donc uniformément continue.
Soient
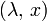
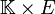
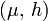
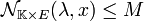
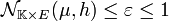
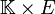
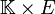
Boule
Cette construction d'une topologie donne toute son importance à la notion de boule ouverte de centre
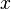

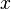

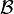
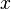

Les boules ouvertes centrées en un point
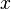
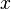
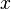
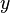
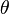
La propriété suivante est donc vérifiée :
Propriété — Un espace vectoriel normé sur R ou C est localement convexe.
Ce qui signifie que tout point admet une base de voisinages convexes, par exemple les boules ouvertes centrées en ce point.
Norme équivalente
Plus la topologie contient d'ouverts, plus précise devient l'analyse associée. Pour cette raison une topologie contenant au moins tous les ouverts d'une autre est dite plus fine. La question se pose dans le cas de deux normes
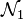
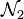
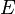
-
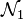
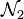
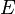
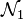
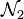
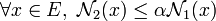
Cette définition est légitimée par le fait que
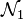
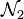
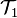
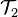
-
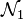
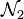
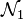
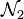
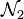
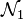
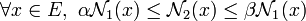
Cela correspond au fait que les boules ouvertes des deux normes puissent s'inclure l'une dans l'autre à dilatation près, ou encore que les deux topologies associées soient les mêmes. En termes métriques, les deux structures sont même uniformément isomorphes. Sur un espace vectoriel réel ou complexe de dimension finie, toutes les normes sont équivalentes (cf topologie d'un espace vectoriel de dimension finie).
Constructions génériques
- Tout produit scalaire sur un espace vectoriel réel E définit la norme euclidienne associée par :
-
-
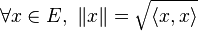
-
- Une norme
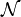
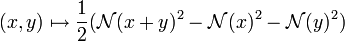
- et dans ce cas cette application est le produit scalaire associé.
- Si f est une application linéaire injective de E dans F alors toute norme sur F induit une norme sur E par l'équation
-
-
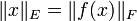
-
- Si C est un ouvert convexe borné et équilibré d'un espace vectoriel réel ou complexe E, alors la jauge de C est une norme définie par
-
-
- et dont C est la boule unité ouverte.
- Si E et F sont deux espaces vectoriels normés réels ou complexes, l'espace
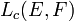
-
-
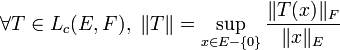
-