Octonion fendu - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Les octonions fendus, comme les octonions, ne sont pas commutatifs ni associatifs. Comme les octonions, aussi, ils forment une algèbre de composition puisque la forme quadratique N est multiplicative. C’est-à-dire,
-
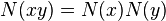
Les octonions fendus satisfont les identités de Moufang et ainsi forment une algèbre alternative. Par conséquent, par le théorème d'Artin, la sous-algèbre générée par deux éléments quelconques est associative. L'ensemble de tous les éléments inversibles (i.e. ces éléments pour lesquels N(x) ≠ 0) forment une boucle de Moufang.
Les octonions hyperboliques
Les octonions fendus sont de manière calculatoire, équivalents aux octonions hyperboliques.
Les octonions fendus en physiques
Les octonions fendus sont utilisés dans la description d'une loi physique, e.g. en théorie des cordes. L'équation de Dirac en physique (l'équation de mouvement d'une particule de spin libre 1/2, comme un électron ou un proton) peut être exprimée avec l'arithmétique des octonions fendus (voir les références ci-dessous).

















































