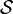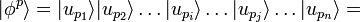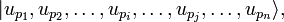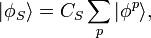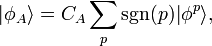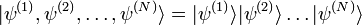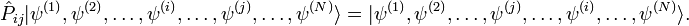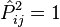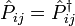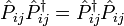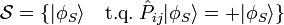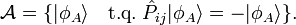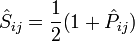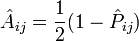Particules indiscernables - Définition

Dégénérescence d'échange

Pour préciser les problèmes liés à l'indiscernabilité des particules, supposons donné un ensemble complet d'observables qui commutent (ECOC) pour une particule et notons la base de constituée des vecteurs propres communs à toutes les observables de cet ECOC. Si le système est composé d'une seule particule, et que l'on mesure toutes les observables de l'ECOC, d'après les postulats de la mécanique quantique, on va projeter l'état du système sur l'un des vecteurs de , de sorte que l'état du système après la mesure sera complètement connu. Supposons maintenant que le système soit composé de deux particules et que l'on effectue une mesure complète de chacune des particules. Le résultat que l'on obtient sera : une particule est dans l'état et l'autre est dans l'état , mais puisqu'on ne peut pas identifier les particules, on ne sait pas laquelle est dans et laquelle est dans . En conséquence, si , le vecteur mathématique de décrivant l'état du système est indéterminé. Ce peut être :

1. ,
2. , en échangeant le rôle des particules par rapport à ci-dessus,
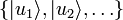
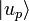
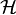
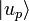
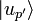
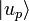
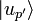
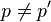
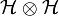
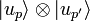
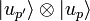
3. ou n'importe quel vecteur de l'espace engendré par ces deux vecteurs.

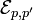
Ainsi, une mesure complète sur chacune des particules ne peut suffire à caractériser complètement l'état du système, ce phénomène étant dénommé dégénérescence d'échange.

Base d'un système de N particules

On cherche à construire le ket d'un système de N particules indiscernables, qui doit être totalement symétrique ou bien antisymétrique. Cela est équivalent à faire une restriction de l'espace vectoriel formé par le produit tensoriel des espaces correspondant à chaque particule.

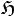
Dans les deux cas, le ket de la fonction d'onde doit être la somme de produit de la forme :

avec toutes les permutations possibles des indices p₁…p_n.

Boson

Pour les bosons, l'état totalement symétrique ne peut être formé qu'à partir d'une combinaison linéaire de tous les états symétriques . On obtient alors le ket suivant :

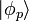
où est la constante de normalisation, calculé à partir de . N_i est le nombre de particules dans le même états. On a bien évidemment

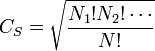
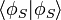
∑	Ni = N
i

.

Fermion

Pour les bosons, l'état totalement antisymétrique ne peut être formé qu'à partir d'une combinaison linéaire de tous les états . On obtient alors le ket suivant :

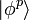
où est la constante de normalisation, calculé à partir de . Ici le terme

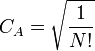
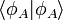
∏	Ni!
i

n'intervient plus car N_i = 0,1 suivant que l'état soit occupé ou non. est la signature de chaque permutation (c'est-à-dire ).

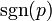
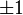
Opérateur de permutation

Définition

Pour construire explicitement les opérateurs de projection et décrits ci-dessus, on introduit l'opérateur qui permet de permuter deux particules dans un système de n particules. En d'autres termes, si

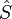
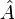
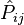
désigne un état factorisable quelconque de l'espace à n particules : , l'opérateur échange l'état de la particule i avec celui de la particule j :

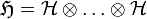
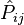
Dans cette définition, nous avons supposé que l'état à n particules était factorisable, ce qui permet de définir l'opérateur sur une base de . Dans un deuxième temps, on étend par linéarité la définition à tous les états de cet espace, y compris les états intriqués.

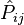
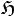
Propriétés

D'après la définition, on a clairement :

On peut aussi montrer que l'opérateur est hermitien et unitaire, soit :

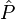
Il possède deux valeurs propres : +1 et -1, auxquelles correspondent deux espaces propres respectivement symétrique et antisymétrique :

Lien avec les opérateurs de symétrie et d'antisymétrie

On définit les opérateurs de symétrie et d'antisymétrie comme :

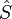
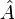
Ces opérateurs sont alors des projecteurs sur les espaces et respectivement.