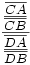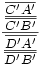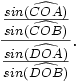Perspective conique - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Notes
Articles connexes
Fondements projectifs des calculs
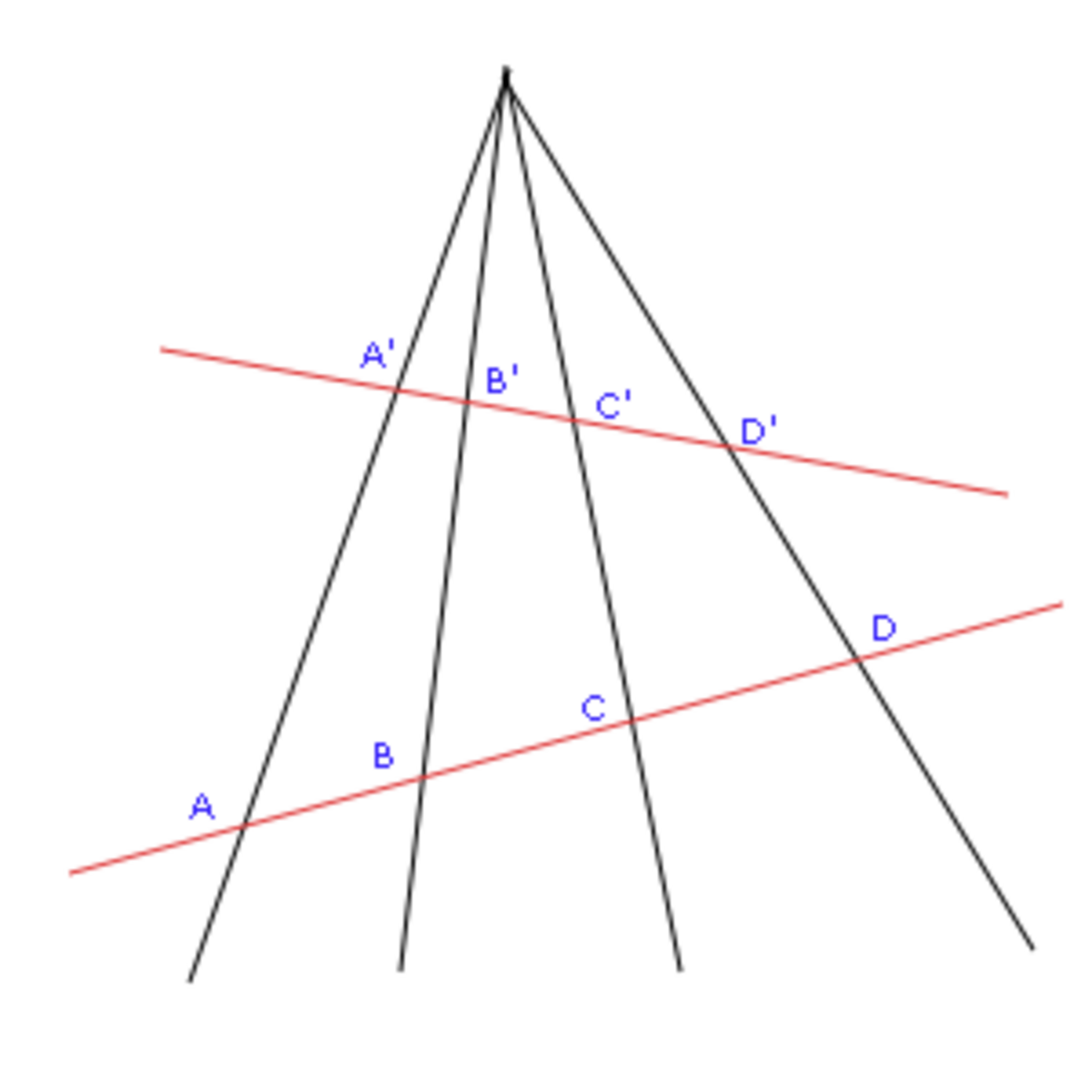
Lorsqu’on projette centralement quatre points alignés sur un plan, peu de choses sont conservées, à part le rapport anharmonique défini ainsi :
qui reste égal à :
et, formule remarquable, est aussi égal au rapport anharmonique des sinus :
De telles équations permettent de simplifier de nombreux calculs.