Perspective conique - Définition

Introduction

La perspective conique a été inventée par Filippo Brunelleschi en 1415 devant le baptistère de Florence. Cette invention a ouvert la voie à la Renaissance artistique.

Exemple

La vue ci-dessus est un tableau de 1475.

Tracés en perspective conique sur un tableau plan

Exemple d'un tracé en perspective conique sur un tableau plan

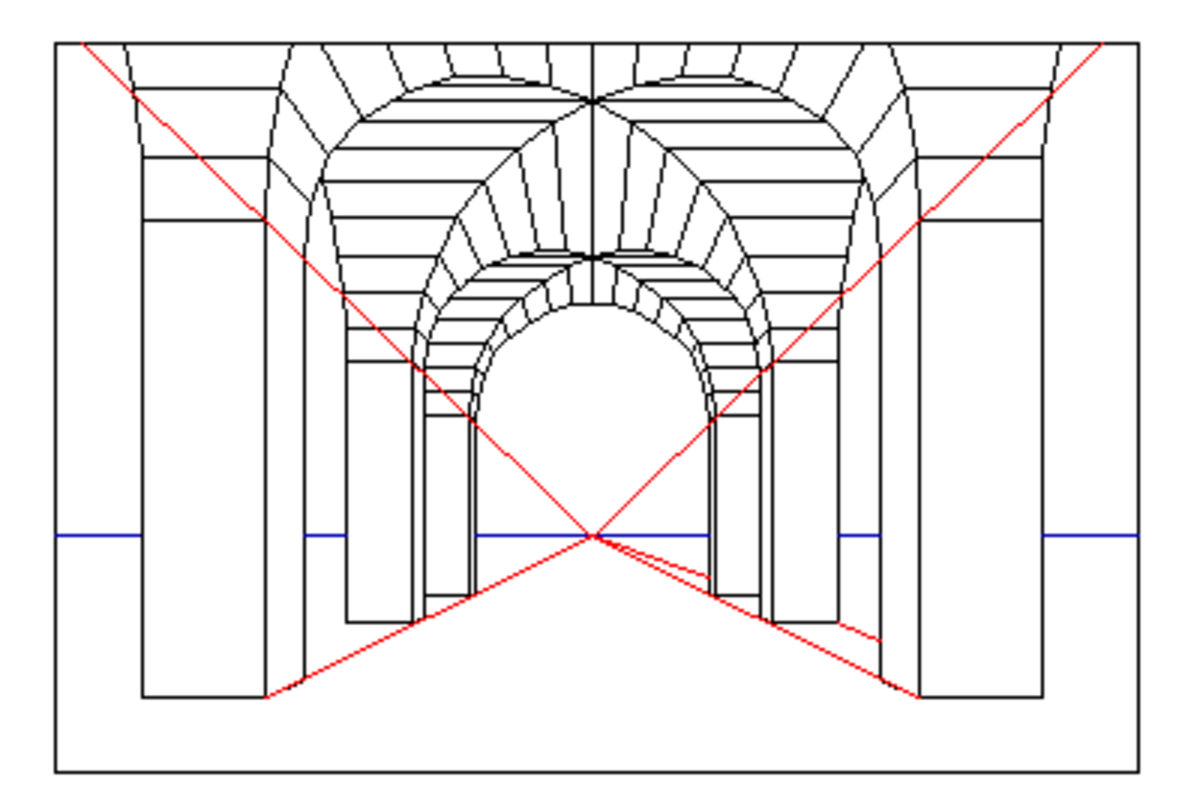
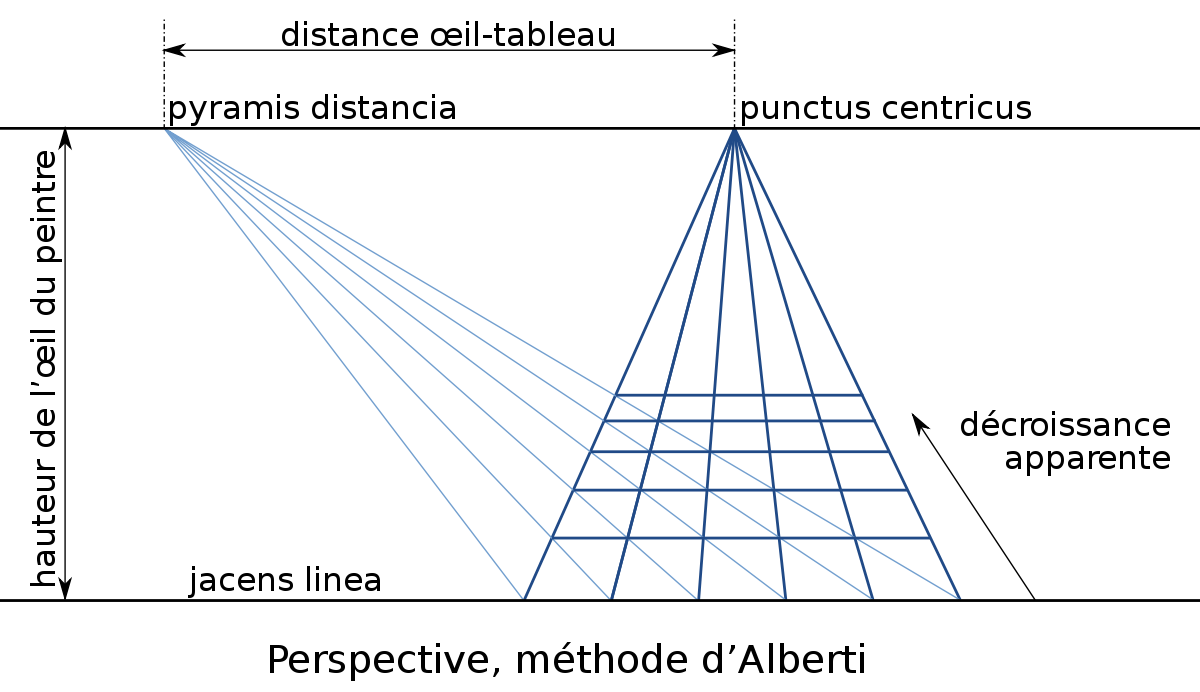
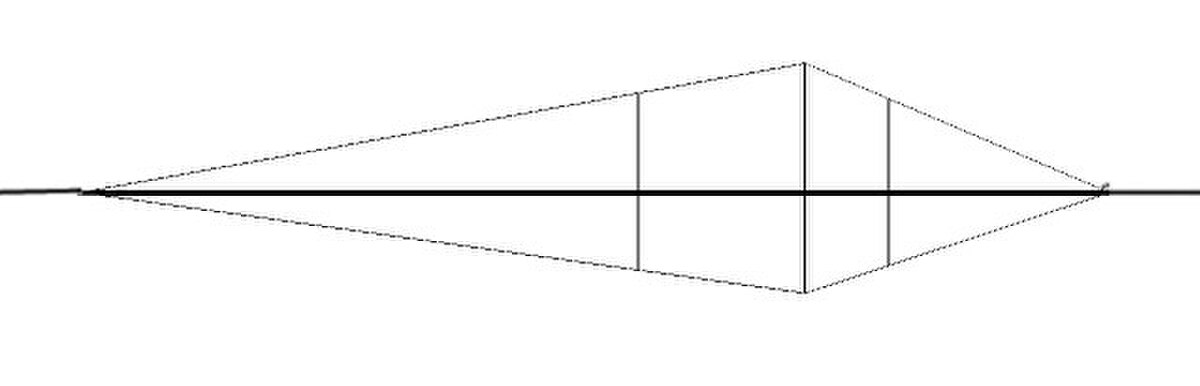
Voici quelques exemples explicatifs de la méthode. La première figure représente l'objet, l'œil et le plan du tableau coupé par des rayons visuels.

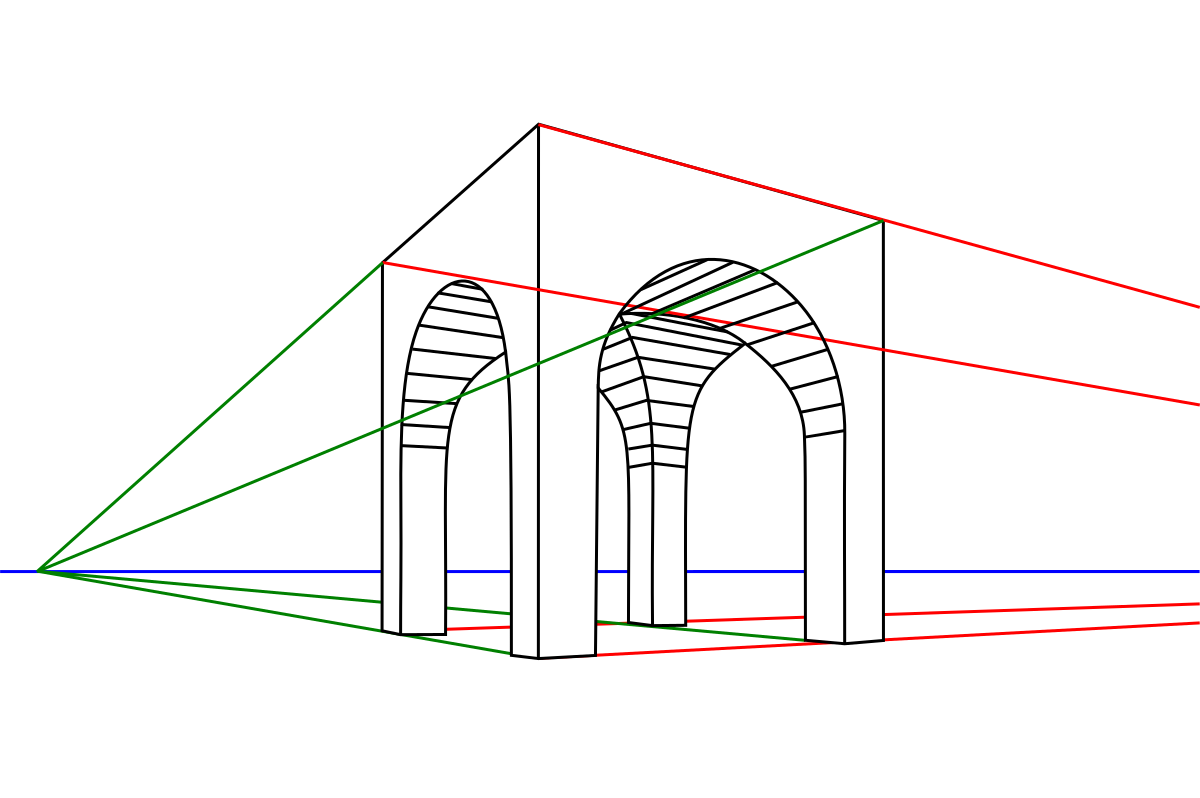
Dans les deux premiers exemples, le plan du tableau est posé verticalement sur le sol. Le premier exemple concerne un objet dont une seule dimension est perpendiculaire au tableau, on n'a qu'un point de fuite. Le deuxième objet est posé en biais par rapport au tableau, ou plutôt le tableau est posé en biais par rapport à l'objet. Dans les deux exemples suivants on prend en compte l'altitude du peintre qui a pour conséquence que le plan du tableau n'est pas vertical mais oblique, d'où il s'ensuit que les lignes verticales de la réalité ne sont pas parallèles au tableau et donc leurs droites projetées convergent soit en bas, soit en haut.

Perspective à un point de fuite

Perspective à 2 points de fuite - Le point de fuite droit sort des limites du tableau.

Perspective à 3 points de fuite (vue en plongée)

Perspective à 3 points de fuite (vue en contre-plongée)

Relation entre les angles dans la perspective à deux points de fuite

La perspective à 2 points de fuite respecte une formule remarquable. Si l'angle de l'objet est de 90°, si G est le point de fuite de gauche, D celui de droite, o le projeté de l'œil du peintre et d la distance œil/tableau, alors oG * oD = - d ² . Ceci, au passage, explique que le plus souvent au moins un point de fuite latéral sort des limites du tableau sinon l'angle de vision serait trop fort et aboutirait à de absurdités latérales. Les règles académiques recommandent de le choisir inférieur à 60°.

La vue suivante, peinte par Perugino est très symétrique et possède un bâtiment central octogonal dont les lignes obliques sont donc à 45° sur le sol. Si on essaie de tracer leur intersection avec la ligne d'horizon on sort largement du cadre, ce qui est bien conforme à la règle de modération de l'angle de vision. Les arcs de triomphe latéraux sont seulement à mi-distance environ des points de distance.

Pérugin, Christ remettant les clés à saint Pierre , 1481-1482, (Chapelle Sixtine)

Différentes perspectives à projection centrale

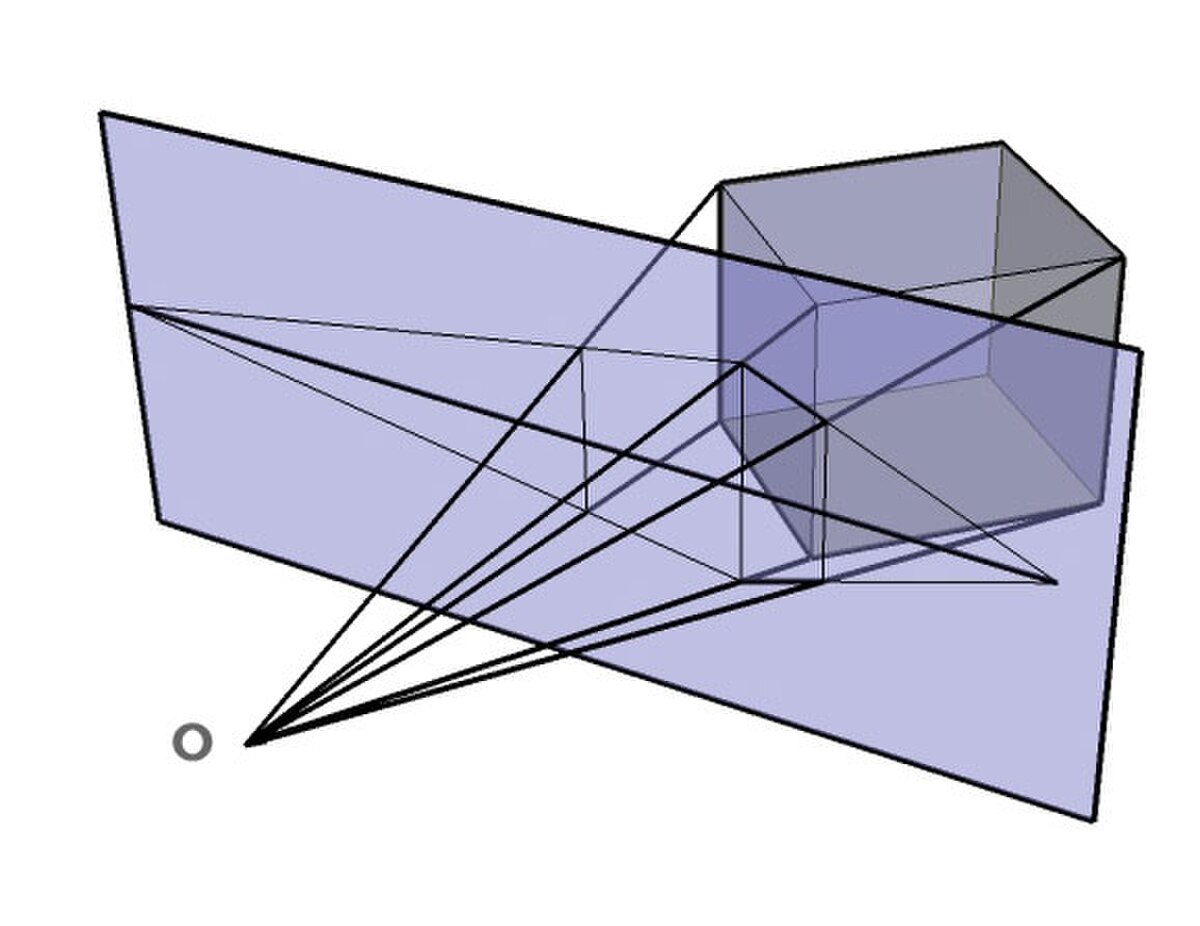
La perspective conique porte son nom du fait que les droites reliant l'œil de l'observateur aux contours d'un objet forment un cône. On parle aussi de projection centrale.

On distinguera en fait plusieurs cas :

• si le tableau est un plan, on obtiendra :
  • une perspective à un point de fuite (si le tableau est parallèle à l'objet à représenter, dans ce cas, certaines droites parallèles seront parallèles dans la perspective),
  • une perspective à deux points de fuite (si le tableau n'est pas parallèle à l'objet à représenter, seules les verticales resteront parallèles entre elles dans la perspective),
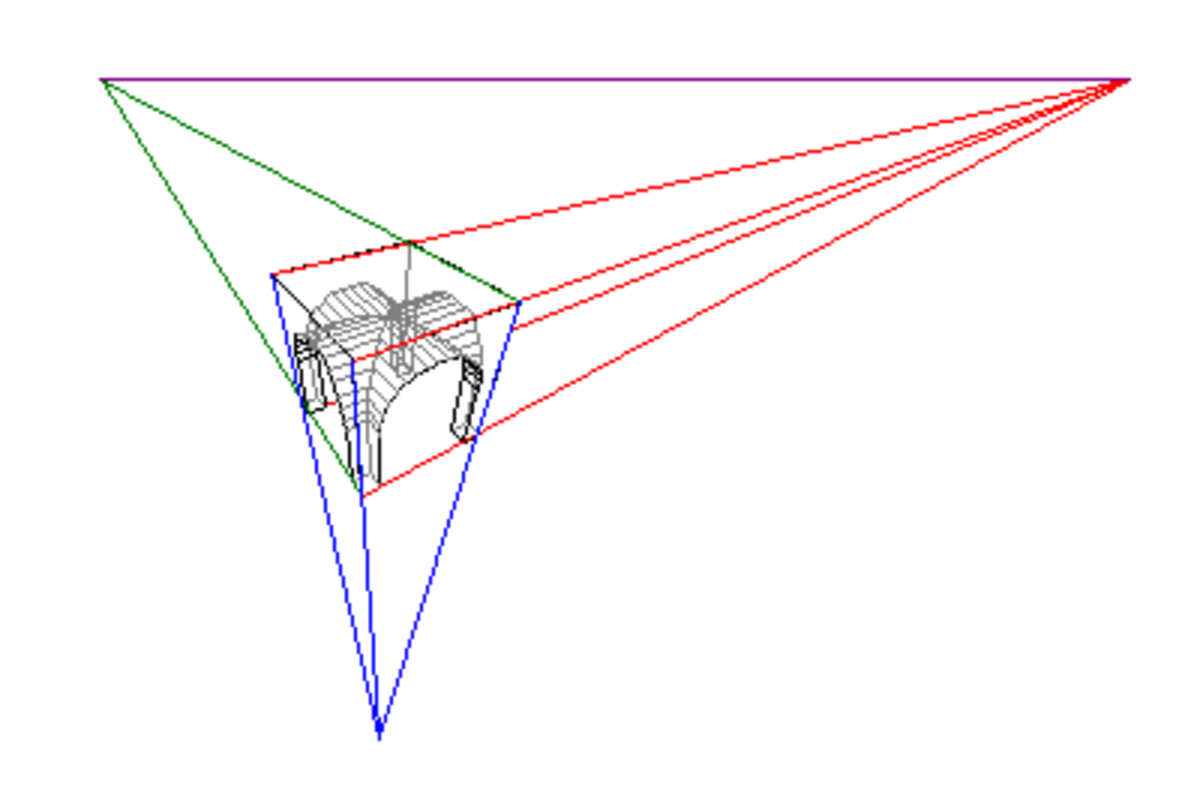
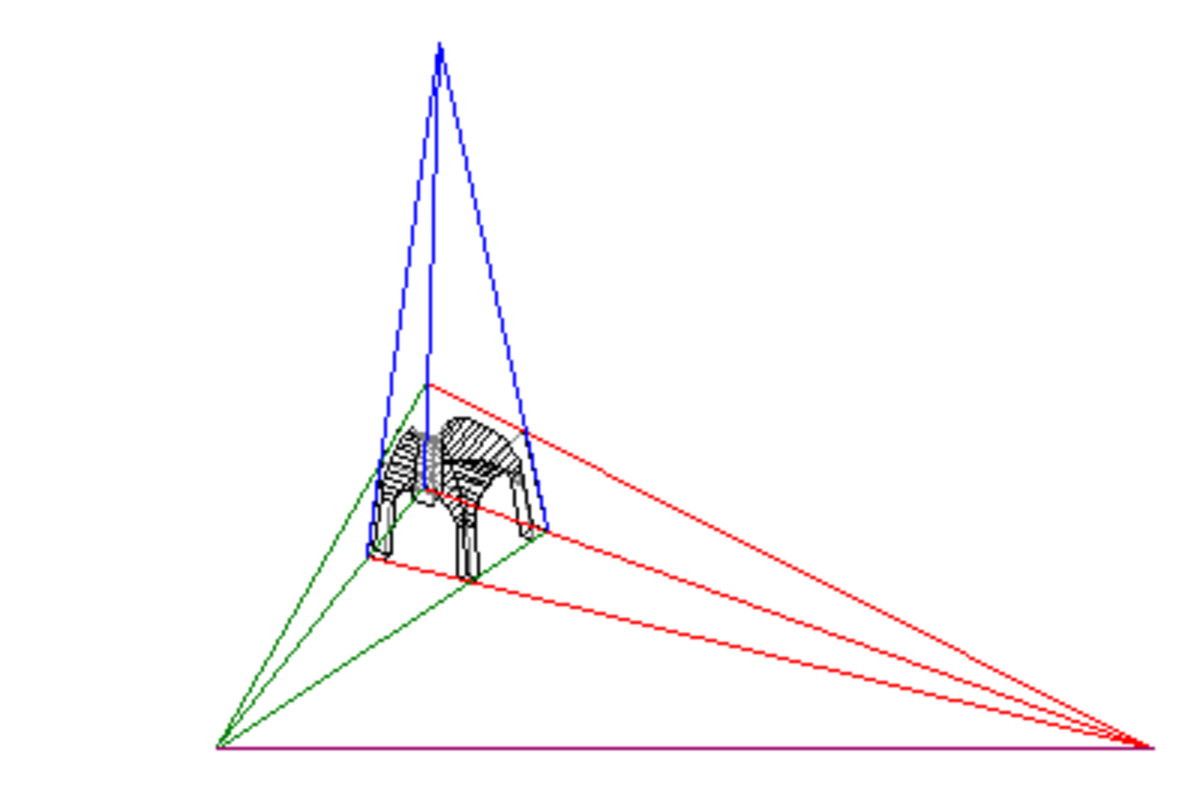
  • une perspective à trois points de fuite (si le tableau n'est pas vertical, alors les verticales ne seront plus parallèles dans la perspective).

Ces distinctions sont valables dans le cas où on voudrait représenter des objets à arêtes parallèles (empilements de parallélépipèdes présentant des arêtes parallèles).

Pour la représentation d'objets de natures différentes, c'est-à-dire pour des objets présentant des lignes situées hors de 3 directions données, il n'y a pas lieu de distinguer de ces divers types de perspectives. Le principe reste le même. Cependant,les perspectives à un point de fuite sont plus faciles à monter à la main, et les perspectives à trois points de fuite sont un casse-tête assez prenant, en accord avec le fait que la représentation d'objets présentant un grand nombre de lignes est plus difficile à effectuer que celle de simples parallélépipèdes. Le traitement informatique de la représentation en perpsective de solides est indépendant du "nombre de points de fuite": Il est toujours mené comme un problème "à trois points de fuite".

• si le tableau est un cylindre, on parlera de perspective cylindrique. On en trouve des prémices dès le Moyen-Âge, M. C. Escher en a fait un de ses outils de prédilection, ils sont indispensables dans les décors lors de travelling en dessin animé. Il s'agit de plans allongés, où 2 points de fuites se trouvent à des points opposés du rectangle du plan. Les points les plus proches ne sont pas reliés au point de fuite par des droites mais par des courbes (arcs de sinusoïdes), les verticales restent verticales dans la perspective. La perspective cylindrique est aussi utilisée pour faire des panoramiques qui peuvent atteindre 360°. Il existe des logiciels qui assemblent plusieurs photos (perspectives planes) pour obtenir un panoramique (perspective cylindrique).
• si le tableau est une sphère, on parlera de perspective sphérique. La perspective sera alors sur une sphère, on ne peut pas la « déplier » comme le cylindre pour le présenter à plat, il faut encore effectuer une projection qui s'apparente à la projection cartographique. Un cas particulier intéressant est la projection stéréographique dans laquelle le centre de projection est sur la sphère et le plan de projection est le plan tangent à la sphère au point opposé à ce centre, cette projection conserve les angles mais pas les distances. Ce type de perspective n'est raisonnablement pas envisageable sans le recours à l'ordinateur.

Exemple : un panoramique 360° dans les sens vertical et horizontal en photo, le logiciel quicktimeVR.uuu.com