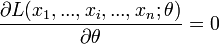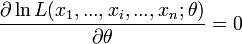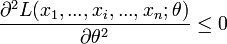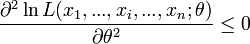Maximum de vraisemblance - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définitions - Propriétés - Généralisation - Exemples

Introduction

L'estimation du maximum de vraisemblance est une méthode statistique courante utilisée pour inférer les paramètres de la distribution de probabilité d'un échantillon donné.

Cette méthode a été développée par le statisticien et généticien Ronald Fisher entre 1912 et 1922.

L'estimateur du maximum de vraisemblance peut exister et être unique, ne pas être unique, ou ne pas exister.

Définitions

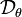
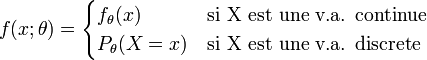
Soit $X$ une variable aléatoire réelle, de loi ou bien discrète ou bien continue, dont on veut estimer un paramètre $θ$ . On note $\mathcal{D}_\theta$ cette famille de lois paramétriques. Alors on définit une fonction $f$ telle que : $f(x;\theta) = \begin{cases} f_\theta(x) & \text{si X est une v.a. continue} \\ P_\theta(X=x) & \text{si X est une v.a. discrete} \end{cases}$

$f θ (x)$ représente la densité de X (où $θ$ apparaît) et $P θ (X = x)$ représente une probabilité discrète (où $θ$ apparaît).

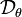
On appelle vraisemblance de $θ$ au vu des observations $(x 1,..., x i,..., x n)$ d'un n-échantillon indépendamment et identiquement distribué selon la loi $\mathcal{D}_\theta$ , le nombre :

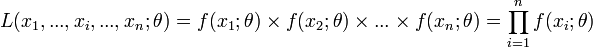
$L(x_1,...,x_i,...,x_n;\theta) = f(x_1;\theta) \times f(x_2;\theta) \times ...\times f(x_n;\theta) = \prod_{i=1}^n f(x_i;\theta)$

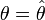
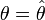
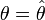
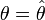
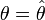
On cherche à trouver le maximum de cette vraisemblance pour que les probabilités des réalisations observées soient aussi maximum. Ceci est un problème d'optimisation. On utilise généralement le fait que si L est dérivable (ce qui n'est pas toujours le cas) et si L admet un maximum global en une valeur $\theta = \hat \theta$ , alors la dérivée première s'annule en $\theta = \hat \theta$ et que la dérivée seconde est négative. Réciproquement, si la dérivée première s'annule en $\theta = \hat \theta$ et que la dérivée seconde est négative en $\theta = \hat \theta$ , alors $\theta = \hat \theta$ est un maximum local (et non global) de $L (x 1,..., x i,..., x n;θ)$ . Il est alors nécessaire de vérifier qu'il s'agit bien d'un maximum global. La vraisemblance étant positive et le logarithme népérien une fonction croissante, il est équivalent et souvent plus simple de maximiser le logarithme népérien de la vraisemblance (le produit se transforme en somme, ce qui est plus simple à dériver). On peut facilement construire la statistique $Y n = Θ$ qui est l'estimateur voulu.

Ainsi en pratique :

La condition nécessaire

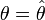
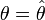
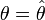
permet de trouver la valeur $\theta = \hat \theta$ .

$\theta = \hat \theta$ est un maximum local si la condition suffisante est remplie au point critique $\theta = \hat \theta$ :

Pour simplifier, dans les cas de lois continues, où parfois la densité de probabilité est nulle sur un certain intervalle, on peut omettre d'écrire la vraisemblance pour cet intervalle uniquement.

Propriétés

L'estimateur obtenu par la méthode du maximum de vraisemblance est :

convergent, mais il peut être biaisé en échantillon fini.
asymptotiquement efficient, il atteint la borne de Cramer Rao.
asymptotiquement distribué selon une loi normale.

Généralisation

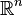
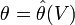
Pour une variable aléatoire réelle X de loi quelconque définie par une fonction de répartition F(x), on peut considérer des petits voisinages V autour de (x₁,..., x_n) dans $\mathbb{R}^n$ , par exemple une boule de rayon ε. On obtient ainsi une fonction de vraisemblance $L(\theta; V) = P[(X_{1,\theta}, ..., X_{n,\theta}) \in V]$ dont on cherche un maximum $\theta = \hat \theta(V)$ . 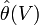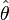On fait ensuite tendre la taille de V vers 0 dans $\hat \theta(V)$ pour obtenir l'estimateur $\hat \theta$ de maximum de vraisemblance.

On retombe sur les fonctions de vraisemblance précédentes quand X est à loi discrète ou continue.

Exemples

Avec une loi discrète

On souhaite estimer le paramètre $λ$ d'une loi de Poisson à partir d'un n-échantillon.

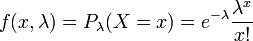
$f(x,\lambda) = P_\lambda(X=x) = e^{-\lambda} \frac{\lambda^x}{x!}$

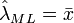
L'estimateur du maximum de vraisemblance est : $\hat {\lambda}_{ML}= \bar x$

La vraisemblance s'écrit :

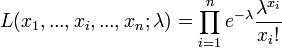
$L(x_1,...,x_i,...,x_n;\lambda) = \prod_{i=1}^n e^{-\lambda} \frac{\lambda^{x_i}}{x_i!}$

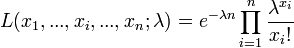
$L(x_1,...,x_i,...,x_n;\lambda) = e^{-\lambda n} \prod_{i=1}^n \frac{\lambda^{x_i}}{x_i!}$

La vraisemblance étant positive, on considère son Logarithme naturel :

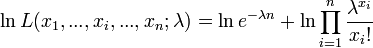
$\ln L(x_1,...,x_i,...,x_n;\lambda) = \ln e^{-\lambda n} + \ln \prod_{i=1}^n \frac{\lambda^{x_i}}{x_i!}$

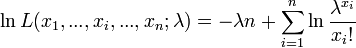
$\ln L(x_1,...,x_i,...,x_n;\lambda) = - \lambda n + \sum_{i=1}^n \ln \frac{\lambda^{x_i}}{x_i!}$

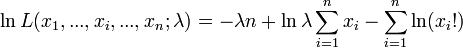
$\ln L(x_1,...,x_i,...,x_n;\lambda) = - \lambda n + \ln \lambda \sum_{i=1}^n x_i - \sum_{i=1}^n \ln (x_i!)$

La dérivée première s'annule quand :

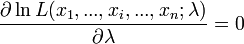
$\frac{\partial \ln L(x_1,...,x_i,...,x_n;\lambda)}{\partial \lambda} = 0$

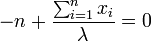
$-n + \frac{\sum_{i=1}^n x_i}{\lambda} = 0$

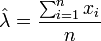
$\hat \lambda = \frac{\sum_{i=1}^n x_i}{n}$

La dérivée seconde s'écrit :

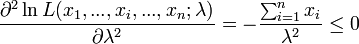
$\frac{\partial^2 \ln L(x_1,...,x_i,...,x_n;\lambda)}{\partial \lambda^2} = - \frac{\sum_{i=1}^n x_i}{\lambda^2} \le 0$

Ce ratio étant toujours négatif alors, l'estimation est donnée par :

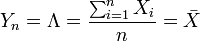
$Y_n = \Lambda = \frac{\sum_{i=1}^n X_i}{n} = \bar X$

Il est tout à fait normal de retrouver dans cet exemple didactique la moyenne empirique, car c'est le meilleur estimateur possible pour le paramètre $λ$ (qui représente aussi l'espérance d'une loi de Poisson).

Avec une loi continue

Loi exponentielle

On souhaite estimer le paramètre $α$ d'une loi exponentielle à partir d'un n-échantillon.

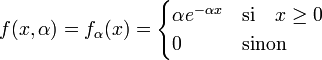
$f(x,\alpha) = f_\alpha(x) = \begin{cases} \alpha e^{-\alpha x} & \text{si} \quad x \ge 0 \\ 0 & \text{sinon} \end{cases}$

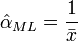
L'estimateur du maximum de vraisemblance est : $\hat {\alpha}_{ML}= \frac{1}{\bar x}$

La vraisemblance s'écrit :

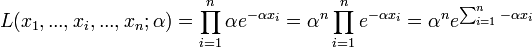
$L(x_1,...,x_i,...,x_n;\alpha) = \prod_{i=1}^n \alpha e^{-\alpha x_i} = \alpha^n \prod_{i=1}^n e^{-\alpha x_i} = \alpha^n e^{\sum_{i=1}^n -\alpha x_i}$

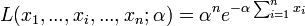
$L(x_1,...,x_i,...,x_n;\alpha) = \alpha^n e^{-\alpha \sum_{i=1}^n x_i}$

La vraisemblance étant positive, on considère son logarithme népérien:

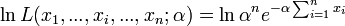
$\ln L(x_1,...,x_i,...,x_n;\alpha) = \ln \alpha^n e^{-\alpha \sum_{i=1}^n x_i}$

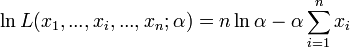
$\ln L(x_1,...,x_i,...,x_n;\alpha) = n \ln \alpha - \alpha \sum_{i=1}^n x_i$

La dérivée première s'annule quand :

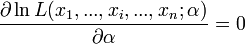
$\frac{\partial \ln L(x_1,...,x_i,...,x_n;\alpha)}{\partial \alpha} = 0$

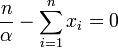
$\frac{n}{\alpha} - \sum_{i=1}^n x_i = 0$

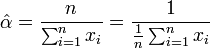
$\hat \alpha = \frac{n}{\sum_{i=1}^n x_i} = \frac{1}{\frac {1}{n} \sum_{i=1}^n x_i}$

La dérivée seconde s'écrit :

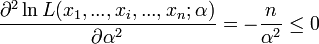
$\frac{\partial^2 \ln L(x_1,...,x_i,...,x_n;\alpha)}{\partial \alpha^2} = - \frac{n}{\alpha^2} \le 0$

Ce ratio est toujours négatif donc l'estimation est donnée par:

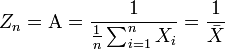
$Z_n = \Alpha = \frac{1}{\frac {1}{n} \sum_{i=1}^n X_i} = \frac{1}{\bar X}$

Là encore, il est tout à fait normal de retrouver l'inverse de la moyenne empirique, car on sait que l'espérance d'une loi exponentielle correspond à l'inverse du paramètre $α$ .

Loi normale

L'estimateur du maximum de vraisemblance de l'espérance $μ$ et la variance $σ 2$ d'une loi normale est:

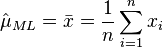
$\hat{\mu}_{ML} = \bar{x} = \frac{1}{n}\sum^{n}_{i=1}x_i$

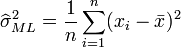
$\widehat{\sigma}^2_{ML} = \frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2$

Une loi normale

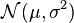
$\mathcal{N}(\mu, \sigma^2)$ a la fonction de densité:

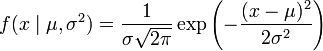
$f(x\mid \mu,\sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} \exp{\left(-\frac {(x-\mu)^2}{2\sigma^2} \right)}$

la fonction de vraisemblance pour un échantillon de n valeurs indépendantes :

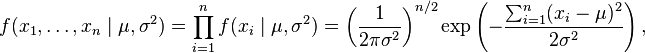
$f(x_1,\ldots,x_n \mid \mu,\sigma^2) = \prod_{i=1}^{n} f( x_{i}\mid \mu, \sigma^2) = \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left( -\frac{ \sum_{i=1}^{n}(x_i-\mu)^2}{2\sigma^2}\right),$

qui peut s'écrire plus simplement (voir Théorème de König-Huyghens):

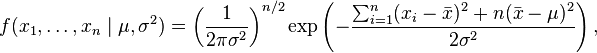
$f(x_1,\ldots,x_n \mid \mu,\sigma^2) = \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left(-\frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2}\right),$

où $\bar{x}$ représente la moyenne de l'échantillon.

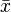
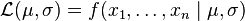
Nous avons là deux paramètres: $θ = μ,σ 2$ , donc il faut maximiser la fonction $\mathcal{L} (\mu,\sigma) = f(x_1,\ldots,x_n \mid \mu, \sigma)$ selon les deux paramètres.

On va donc chercher la dérivée première et l'égaliser à zéro.

En l'occurrence, c'est la fonction de log-vraisemblance qui est maximisée ici.

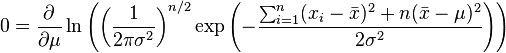
$0 = \frac{\partial}{\partial \mu} \ln \left( \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left(-\frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2}\right) \right)$

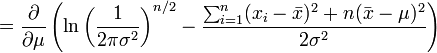
$= \frac{\partial}{\partial \mu} \left( \ln\left( \frac{1}{2\pi\sigma^2} \right)^{n/2} - \frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2} \right)$

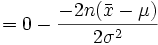
$= 0 - \frac{-2n(\bar{x}-\mu)}{2\sigma^2}$

et on obtient donc l'estimateur par le maximum de vraisemblance de l'espérance:

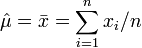
$\hat\mu = \bar{x} = \sum^{n}_{i=1}x_i/n$

On peut montrer en plus que cet estimateur sans biais:

$\mathbb{E} \left[ \widehat\mu \right] = \mu$

Pour le second paramètre, σ, on cherche par analogie le maximum en fonction de σ.

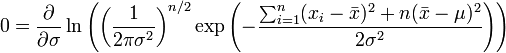
$0 = \frac{\partial}{\partial \sigma} \ln \left( \left( \frac{1}{2\pi\sigma^2} \right)^{n/2} \exp\left(-\frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2}\right) \right)$

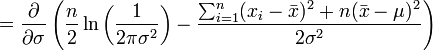
$= \frac{\partial}{\partial \sigma} \left( \frac{n}{2}\ln\left( \frac{1}{2\pi\sigma^2} \right) - \frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{2\sigma^2} \right)$

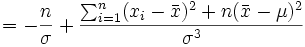
$= -\frac{n}{\sigma} + \frac{ \sum_{i=1}^{n}(x_i-\bar{x})^2+n(\bar{x}-\mu)^2}{\sigma^3}$

donc

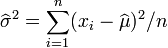
$\widehat\sigma^2 = \sum_{i=1}^n(x_i-\widehat{\mu})^2/n$

et on obtient finalement l'estimateur par le maximum de vraisemblance de la variance:

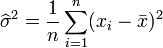
$\widehat\sigma^2 = \frac{1}{n} \sum_{i=1}^{n} (x_{i} - \bar{x})^2$

L'estimateur de la variance est par contre biaisé :

$\mathbb{E} \left[ \widehat{\sigma^2} \right]= \frac{n-1}{n}\sigma^2$

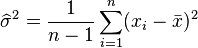
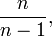
L'estimateur de la variance est un bon exemple pour montrer que le maximum de vraisemblance peut fournir des estimateurs biaisés : un estimateur sans biais est donné en effet par: $\widehat\sigma^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{x})^2$ . Néanmoins, asymptotiquement, quand n tend vers l'infini, ce biais, qui est de $\frac{n}{n-1},$ tend vers 1 et l'estimateur est alors asymptotiquement sans biais.

Si la dérivée ne s'annule jamais

On souhaite estimer le paramètre a d'une loi uniforme à partir d'un n-échantillon.

$f(x,a) = f_a(x) = \begin{cases} \frac {1}{a} & \text{si} \quad x \in [0;a] \\ 0 & \text{sinon} \end{cases}$

La vraisemblance s'écrit :

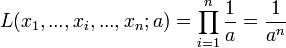
$L(x_1,...,x_i,...,x_n;a) = \prod_{i=1}^n \frac {1}{a} = \frac {1}{a^n}$

Intuitivement, il est clair que cette expression de la vraisemblance ne s'annule jamais (on peut la dériver pour s'en convaincre). Graphiquement dans le repère (a, L), sa représentation est une courbe décroissante de type « inverse » (convexe tournée vers l'origine).

La valeur de L sera maximale quand a sera très près de 0, donc quand a sera le plus petit possible (l'intervalle de la densité est alors réduit). Mais, pour que la densité soit vraie, le paramètre a doit être nécessairement plus grand que tous les $x i$ de l'échantillon.

On prend donc comme valeur qui maximise L, tout en vérifiant la définition de la loi de probabilité :

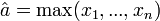
$\hat a = \max(x_1,...,x_n)$

$W n = A = max(X 1,..., X n)$

Cet exemple permet de montrer, qu'un estimateur n'est pas toujours défini par une expression numérique explicite. Ainsi on sera amené parfois à considérer le maximum ou le minimum des échantillons.

- Introduction - Définitions - Propriétés - Généralisation - Exemples

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Ce plat millénaire réduit significativement la graisse corporelle 🍽️

Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭

Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠

De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽

Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️

Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐

Une montagne d'or découverte en Chine ⛏️

Cette simulation de l'Univers est totalement vertigineuse 🌀

Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘

Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️

Voici pourquoi votre enfant triche et ce que cela révèle 🧠

Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱

Neuralink: un bras robotique contrôlé par la pensée 🦾

Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀

L'étonnant impact du froid sur notre sommeil ❄️

Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️

Créer des souris à partir d'un gène plus vieux que les animaux eux-mêmes: une expérience inédite 🧬

Pourquoi tant de noms de drogues finissent par "ine" ou "is" ? ☠️

L'impact étonnant de la régularité de votre heure de coucher sur votre cœur 💔

Quand l'IA se prend pour Jésus dans un confessionnal: cette chapelle fait débat 🤔

Un diagnostic universel de toutes les maladies infectieuses, connues et inconnues, en un seul test 🧪

Consommer ce champignon ralentirait la progression du cancer 🍄

Découverte: les égyptiens consommaient un cocktail hallucinogène contenant... du sang humain 🩸

Page générée en 0.438 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise