Principe de moindre action et relativité restreinte - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En relativité restreinte, le principe de moindre action donne des équations d'Euler-Lagrange presque inchangées par rapport à celles de la mécanique classique, mais le lagrangien n'est plus égal à la différence entre l'énergie cinétique et l'énergie potentielle. En fait, à partir de la relativité, il est apparu que le principe de moindre action se base sur l'existence d'une trajectoire continue, paramétrée par le temps, qui minimise une fonction ou la différence entre des fonctions du système étudié, déterminées à partir de principes généraux, tels que par exemples :
- Comme la trajectoire dans l'espace-temps ne dépend pas du repère d'où on l'observe, l'action qui la détermine, ainsi que les fonctions qui composent l'action, sont invariantes par changement de repère.
- L'indépendance de corps implique l'additivité de leurs actions et de leurs lagrangiens, pour que les trajectoires puissent être déterminées séparément en appliquant la méthode variationnelle.
Il se trouve qu'en physique classique, ces fonctions du système sont les énergies cinétiques et potentielles, ce n'est plus le cas en relativité.
En physique relativiste, et en l'absence de champ électromagnétique, on montre que la fonction du corps qui est minimisée dans le principe est particulièrement simple : il s'agit de − mcτ, où τ est « temps propre » du trajet, qui est à la fois le temps s'écoulant dans le référentiel du corps au cours du trajet et la longueur de la trajectoire mesurée par la métrique de l'espace : cela revient à maximiser le « temps propre », du fait du signe − et de la constance de la masse m et de la vitesse de la lumière c.
Un champ électromagnétique amène des différences de parcours entre les corps, suivant leurs charges et leurs répartitions.
Et comme en physique classique, toutes les équations peuvent être obtenues sans le principe de moindre action.
Le lecteur doit prendre garde que dans cet article, on n'étudie que le potentiel du champ électromagnétique, et la lettre 
désigne une vitesse, ainsi qu'indiqué ci-dessous.
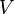
Avec ou sans quadri-écriture
- En relativité restreinte, les corps évoluent dans l'espace-temps de Minkowski où chaque référentiel galiléen a ses coordonnées d'espace
et sa coordonnée de temps 
, subissant toutes une modification en cas de changement de référentiel galiléen. Il n'y a donc plus de temps absolu, pourtant le temps d'un référentiel quelconque, galiléen ou non, permet toujours de paramétrer l'évolution d'un système physique.
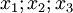
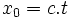
- En choisissant de repérer le système dans un référentiel galiléen quelconque, donc avec les coordonnées
, on peut choisir un temps t0 d'un autre référentiel quelconque, galiléen ou non, pour paramétrer son évolution.
- Le lagrangien
exprimé à l'aide des coordonnées et de la vitesse peut donc s'écrire 
, avec 
.
- Si on choisit
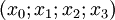
le temps du référentiel des coordonnées, le lagrangien et les équations qui en sont tirées donnent, à l'approximation aux petites vitesses devant 
, le lagrangien et les propriétés de la mécanique classique. On dira alors travailler sans la quadri-écriture car seules les coordonnées spatiales apparaissent en général. - Si on choisit
le temps propre, avec 
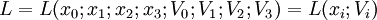
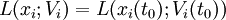
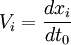
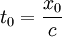
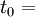
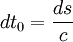
, on obtient des résultats équivalents mais dont l'écriture est jugée plus élégante et s'approche de celle de la relativité générale. On remarquera qu'un repère propre n'est galiléen que si le corps est libre. Avec le temps propre, on dira travailler en quadri-écriture car les quatre coordonnées du référentiel apparaissent dans les calculs. - Si on choisit t0 un temps autre quelconque, on peut travailler plus facilement avec les dérivées partielles qu'en utilisant les deux autres temps précédents; mais les résultats, bien qu'équivalents, ont une écriture moins maniable et moins élégante. Dans ce cas, on dira aussi travailler en quadri-écriture, pour la même raison.
- Avec la quadri-écriture
Par commodité, nous adopterons la convention de sommation d'Einstein dans l'espace de Minkowski : pour deux quadri-vecteurs 
et 
, on définit le produit scalaire 
par 
, avec 
et pour i=1;2;3 
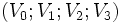
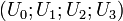
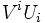
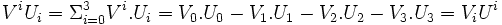
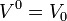
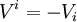
On a alors : 
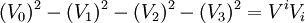
On montre que : 
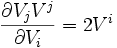
De manière similaire, on écrira : 
et 
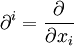
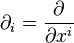
En utilisant un temps quelconque indéterminé 
, l'action 
permet d'obtenir les équations d'Euler-Lagrange, relativistes mais obtenues de la même manière que dans le cas classique, avec une coordonnées de plus :
pour j=0;1;2;3
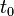
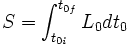
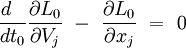
Il est important de remarquer que comme dans le cas classique, l'action et le lagrangien ne sont pas définis de manière unique : l'action est définie à l'addition près d'une fonction des extrémités du trajet et du temps, et le lagrangien est défini à l'addition près de la dérivée d'une fonction du temps (qui une fois intégrée donne une fonction des extrémités et du temps).