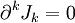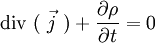Principe de moindre action et relativité restreinte - Définition
La liste des auteurs de cet article est disponible ici.
Cas d'un champ « de force »
En physique classique, l'influence d'un corps sur un autre se transmet instantanément ; avec l'arrivée de l'électromagnétisme de Maxwell et plus encore avec celle de la relativité restreinte, l'influence se transmet au maximum à la vitesse de la lumière (dans le vide).
Ainsi, entre le corps influent et le corps influencé, il se balade quelque chose dans l'espace, en général à la vitesse de la lumière, qui se répand dans l'espace et dont l'effet est un changement de trajectoire du corps influencé.
Suivant quelles propriétés ce champ (appelé ainsi car il a tendance à occuper l'espace) est-il créé, se déplace-t'il, est-il influencé par son environnement, etc ?
On peut répondre à ces questions à l'aide du principe de moindre action.
Densité lagrangienne et équations d'Euler-Lagrange associées
- Un champ est caractérisé par une étendue importante dans l'espace, on ne peut donc pas le repérer par les coordonnées
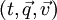
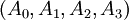
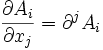
- Nous utiliserons donc
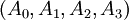
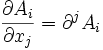
- L'action d'un champ est donc de la forme :
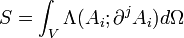
- Où V est le quadri-volume dans lequel on va appliquer la méthode variationnelle,
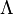
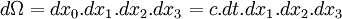
- Par une démonstration semblable à celle déjà vue dans le cas d'un corps localisable, et en utilisant la convention de sommation d'Einstein, on obtient les équations d'Euler-Lagrange pour la densité lagrangienne :
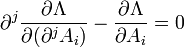
Tenseur impulsion-énergie d'un champ
La densité lagrangienne
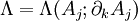
On a :
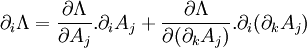
le lemme de Schwarz et enfin l'égalité
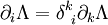
on obtient :
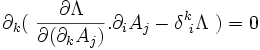
en posant
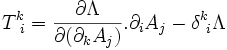
tenseur « impulsion-énergie », on a :
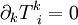
ce qui exprime sa conservation.
En posant :
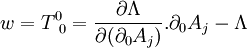
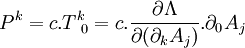
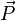
Nous avons alors les deux équations équivalentes
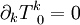
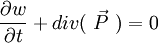
qui est l' « équation de conservation de l'énergie » : localement, la variation dans le temps de la densité d'énergie
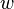
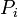
Densité lagrangienne d'un champ électromagnétique libre
La densité lagrangienne du champ électromagnétique est :
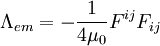
- On cherche la densité lagrangienne du champ électromagnétique qui est composé du ou des nombres construits à partir du potentiel électromagnétique
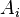
- La manifestation de ce potentiel est le champ électrique =
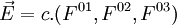
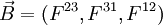
- On cherche donc les nombres invariants construits à partir de la matrice 4×4 associée :
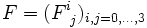
- Les coefficients du polynôme caractéristique sont invariants par la transformation d'endomorphismes
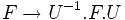
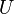
- Les invariants de cette matrice par les changements de base sont les coefficients de son polynôme caractéristique
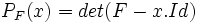
- On sait, par la définition de ses coefficients, que cette matrice est anti-symétrique :
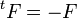
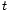
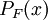
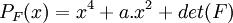
- Par quelques calculs, on montre que
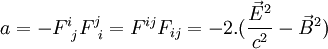
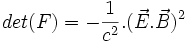
- Il y a donc deux nombres à examiner :
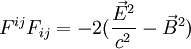
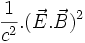
- Pour une raison de dimension , le nombre
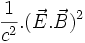
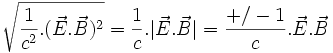
- Mais on peut montrer que
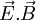
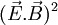
- De ce fait,
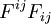
- En choisissant un coefficient multiplicateur qui détermine les unités de mesure du champ électromagnétique, on prend :
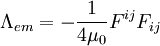
- le signe

Les équations du champ électromagnétique
L'hypothèse de ce paragraphe est qu'il y a un courant de particules (voire d'une seule particule) non influencé par le champ électromagnétique. Avec cette condition, on étudie les modifications du champ.
On sait (par hypothèse) que l'interaction entre une particule et le champ se modélise, sous forme lagrangienne, par
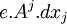
L'action est donc :
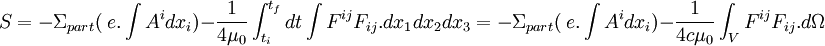
On a :
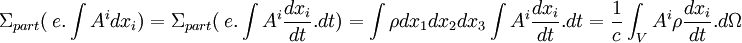
Ce que l'on peut écrire :
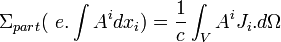
Avec
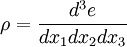
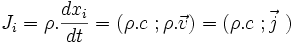
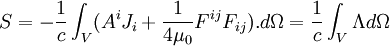
La densité lagrangienne à utiliser est :
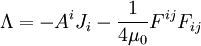
Les équations d'Euler-Lagrange donnent :
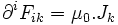
Pour k = 0 , on obtient
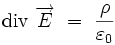
Pour k∈{1;2;3} on obtient
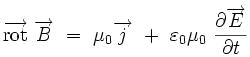
De plus, à partir de
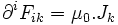
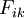
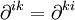
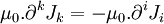
D'où les deux présentations de « l'équation de conservation de la charge » :