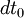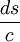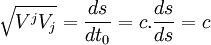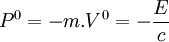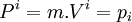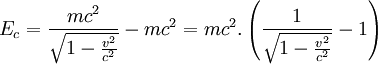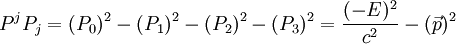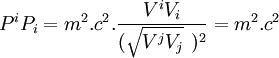Principe de moindre action et relativité restreinte - Définition

Cas d'un corps libre

Lagrangien d'un corps libre

Déterminons l'action et le lagrangien relativiste d'un corps libre.

Dans aucun référentiel galiléen la quadri-vitesse n'est nulle car le corps avance au moins dans la dimension temporelle.

Le lagrangien relativiste d'un corps libre doit, aux petites vitesses et en première approximation, être égal (peut-être à une constante additive près : l'ajout d'une constante ne change pas les équations d'Euler-Lagrange) au lagrangien classique.

Dans l'espace-temps de Minkowski, l'action détermine la trajectoire, et celle-ci ne dépend pas du référentiel d'où on l'observe. Donc l'action ne dépend pas des coordonnées, et, pour un corps libre, dépend seulement de la vitesse et est invariante par les transformations de Lorentz :

est invariant par les transformations de Lorentz

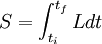
Dans le référentiel propre du corps, est la variation du temps propre du corps ; et la vitesse spatiale du corps est nulle. Dans un référentiel galiléen, et avec l'hypothèse que le corps est libre, la quadri-vitesse est constante dans le temps (et n'est jamais nulle) donc le lagrangien aussi car il dépend de la seule vitesse.

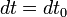
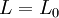
Ainsi, dans le référentiel propre du corps le lagrangien propre, , est une constante dans le temps.

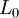
Vu depuis un autre référentiel galiléen, se déplaçant par rapport au référentiel propre à la vitesse spatiale constante, on a :

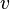
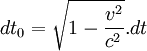
Donc :

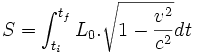
où vitesse spatiale relative entre le référentiel et le référentiel propre du corps = vitesse spatiale du corps dans le référentiel.

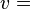
Donc : par l'approximation aux petites vitesses devant .

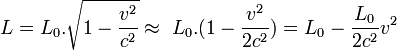
En comparant au lagrangien classique (qui n'est pas réellement modifié par l'ajout de la constante L₀) , on obtient : , d'où

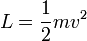
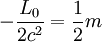
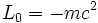
Conclusion : dans un référentiel galiléen quelconque, le lagrangien est

où est la vitesse spatiale du corps dans ce référentiel.

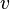
Impulsion et énergie

• Par définition de l'impulsion , on a :

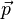
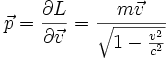
L'énergie est définie par :

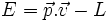
On obtient :

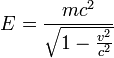
En particulier, pour v = 0, l'énergie au repos est

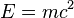
• En exprimant l'énergie en fonction de l'impulsion, on obtient : ou encore

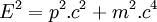
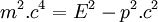
• On remarquera que bien qu'ayant la dimension d'une énergie, le lagrangien relativiste n'est pas l'énergie cinétique : cette dernière vaut

On a bien ≈ à l'approximation aux petites vitesses devant

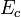
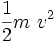
Avec la quadri-écriture

• On constate que , en utilisant l'égalité et la définition adéquate de , appelé « temps propre » du corps.

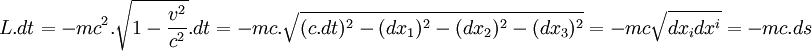
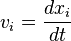
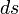
En utilisant le fait que est le temps propre du corps, l'action minimisée entre deux points de l'espace-temps montre que le chemin suivi par la particule pour aller du point A au point B est celui qui maximise le temps propre, car le terme négatif − mc transforme la minimisation de en maximisation de .

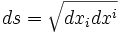
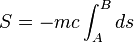
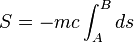
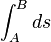
En factorisant par , un temps quelconque paramétrant le système (et n'est donc pas obligatoirement le temps propre), on obtient :

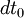
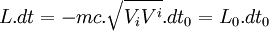
, en utilisant la quadri-vitesse pas obligatoirement propre définie par : ,avec .

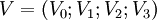
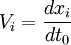
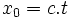
Le lagrangien relativiste d'une particule libre, paramétrée par le temps quelconque , s'exprime donc :

.

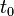
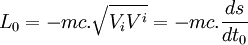
• On se rappelle que la quadri-impulsion, comme l'impulsion, est définie par

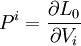
D'où :

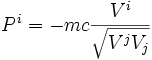
Pour i = 0 , on obtient :

Pour i = 1;2;3 , de manière similaire au cas i=0, on obtient : .

Le carré de la "norme" de la quadri-impulsion est , et aussi

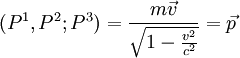
D'où la formule déjà vue :

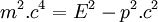
• La constance de la quadri-impulsion, démontrée à partir des équations d'Euler-Lagrange, permet de montrer que l'énergie E et l'impulsion spatiale sont constantes par rapport au temps .

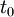
• La constante par rapport au temps est en fait la constante 0 ; une petite manipulation permet d'en déduire l'égalité déjà vue .

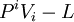
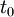
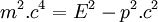
En calculant pour i∈{1;2;3} on retrouve l'énergie et l'égalité déjà citées.

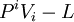
• On montre facilement que quel que soit le temps choisi, s'il est celui d'un repère galiléen, la vitesse et la "pseudo-norme" sont constantes par rapport au temps  : c'est une conséquence directe de la définition des repères galiléens, et du fait que le corps est libre.

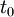
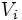
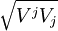
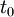
• Dans le cas particulier où est le temps propre , alors les quadri-vitesse et quadri-impulsion sont propres, et on a l'égalité particulière , qui peut être embarrassante pour l'utilisation des dérivées partielles dans le travail ci-dessus, et qui donne et pour i=1;2;3 .