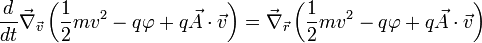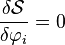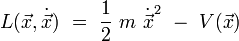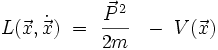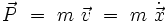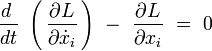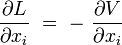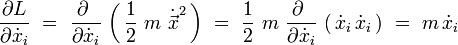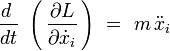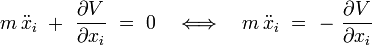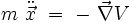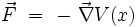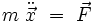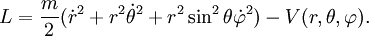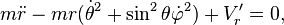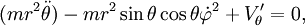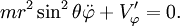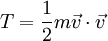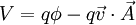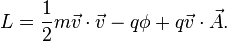Lagrangien - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le lagrangien
![\mathcal{L}[\varphi_i]](https://static.techno-science.net/illustration/Definitions/autres/b/b9c3f5e4b34fb0ba13145ec0678fb4d3_0d96029bf6d1d17aca907479493ef72f.png)
Les équations du mouvement s'obtiennent par application du principe de moindre action (ou principe d'action extrémale), qui s'écrit :
avec l'action
![\mathcal{S}[\varphi_i] = \int{\mathcal{L}[\varphi_i(s)]{}\,d^ns},](https://static.techno-science.net/illustration/Definitions/autres/6/6d1ddad9e9382dec25e2d70071bb51e5_68b4e8d30c0281cf71504c9b8043e195.png)
et
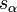
Les équations du mouvement obtenues sont équivalentes aux équations d'Euler-Lagrange. Un système dynamique dont les équations du mouvement peuvent s'obtenir à partir d'un principe de moindre action et d'un lagrangien est un système dynamique lagrangien. C'est le cas de la version classique du modèle standard, des équations de Newton, des équations de la relativité générale, et de problèmes purement mathématiques comme les équations des géodésiques ou le problème de Plateau.
Un exemple en mécanique classique
Le concept de lagrangien fut historiquement introduit dans une reformulation de la mécanique classique, la mécanique lagrangienne. Dans ce contexte, le lagrangien vaut généralement l'énergie cinétique à laquelle on soustrait l'énergie potentielle :
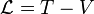
En coordonnées cartésiennes
Le lagrangien d'une particule de masse m non relativiste dans un espace euclidien à trois dimensions s'écrit :
ou bien
avec P la quantité de mouvement
on note la dérivation temporelle par un point au-dessus de la quantité différentiée.
Les équations d'Euler-Lagrange s'écrivent :
L'indice i = 1, 2, 3. Le calcul des dérivées donne :
P=m.v
Les équations d'Euler-Lagrange s'écrivent donc explicitement :
soit sous forme vectorielle :
Les approches lagrangienne et newtonienne sont donc équivalentes lorsque la force dérive d'un potentiel :
puisque la formulation de la deuxième loi de Newton dans un référentiel Galiléen s'écrit :
En coordonnées sphériques
Soit un espace à trois dimensions en coordonnées sphériques
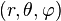
Les équations d'Euler-Lagrange s'écrivent alors :
Ici l'ensemble des paramètres
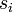
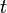
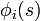
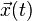
Lagrangien électromagnétique
En général, en mécanique lagrangienne, le lagrangien vaut:
- L = T − V
où T est l'énergie cinétique et V l'énergie potentielle.
Etant donnée une particule chargée électriquement de masse m et charge q, et de vitesse

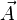
et son énergie potentielle est:
Le lagrangien électromagnétique est alors:
Le lagrangien électromagnétique se construit à partir de l'expression de la force de Lorentz :
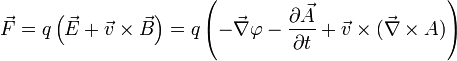
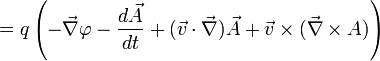
Les deux termes du membre de droite est un gradient d'un produit scalaire, la force est le gradient de l'énergie cinétique (par rapport à la vitesse) dérivée par rapport au temps obtenant :
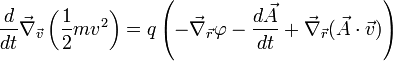
Le reste n'est plus qu'une question d'écriture :