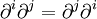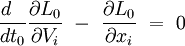Principe de moindre action et relativité restreinte - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Avec ou sans quadri-écriture - Cas d'un corps dans un champ électromagnétique - Cas d'un corps libre - Cas d'un champ « de force »

Cas d'un corps dans un champ électromagnétique

Sans la quadri-écriture

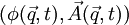
Comme dans le cas classique, le lagrangien peut être défini en utilisant un potentiel électromagnétique $(\phi(\vec{q},t), \vec{A}(\vec{q},t))$ :

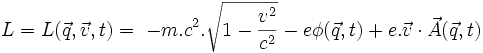
$L = L(\vec{q},\vec{v},t) = \ -m.c^2.\sqrt{1-\frac{v^2}{c^2}} - e\phi(\vec{q},t) + e. \vec{v} \cdot \vec{A}(\vec{q},t)$

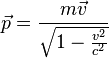
En prenant encore $\vec{p} = \frac{m\vec{v}}{\sqrt{1-\frac{v^2}{c^2}}}$ , les équation d'Euler-Lagrange donnent :

ce qui n'est pas une égalité pratique à utiliser car la dérivation de

est laborieuse.

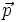
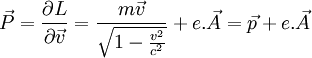
L'impulsion est définie par : $\vec{P} = \frac{ \partial L}{\partial \vec{v}} = \frac{m\vec{v}}{\sqrt{1-\frac{v^2}{c^2}}} + e.\vec{A} = \vec{p} + e.\vec{A}$

On prendra donc soin de distinguer $\vec{p}$ et $\vec{P}$

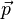
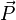
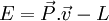
L'énergie est définie par : $\ E = \vec{P}.\vec{v} - L$

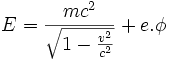
On obtient : $\ E = \frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}} + e.\phi$

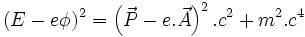
Et après quelques calculs pour exprimer l'énergie en fonction de l'impulsion : $\ (E-e\phi)^2 = \left(\vec{P} - e.\vec{A}\right)^2.c^2 + m^2.c^4$

Toutes les approximations aux petites vitesses devant $c$ redonnent les résultats classiques.

À partir du potentiel électromagnétique, le premier groupe des équations de Maxwell se démontre sans difficulté : l'équation de Maxwell-Faraday et l'équation de conservation du flux magnétique.

Avec la quadri-écriture

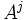
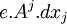
Le champ électromagnétique se manifeste sous forme d'un quadri-vecteur, appelé quadri-potentiel électromagnétique, $\ A^j$ dont l'interaction avec la particule de charge $\ e$ se manifeste sous forme lagrangienne par $\ e.A^j.dx_j$

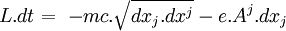
La définition de l'action relativiste infinitésimale d'un champ électromagnétique est donc $\ L.dt = \ -mc.\sqrt{dx_j.dx^j} - e.A^j.dx_j$ .

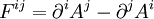
On pose $F^{ij} = \partial^i A^j - \partial^j A^i$ tenseur champ électromagnétique.

En prenant $\ t_0$ le temps propre de la particule, les équations d'Euler-Lagrange donnent les équations du mouvement de la particule :

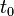
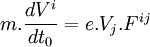
$m. \frac{dV^i}{dt_0} = e.V_j.F^{ij}$

Que l'on peut écrire aussi :

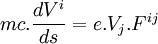
$mc. \frac{dV^i}{ds} = e.V_j.F^{ij}$

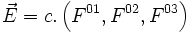
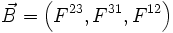
En prenant : champ électrique = $\vec{E} = c.\left(F^{01},F^{02},F^{03}\right)$ et champ magnétique = $\vec{B} = \left(F^{23},F^{31},F^{12}\right)$ , on retrouve la force de Lorentz sous son écriture habituelle.

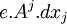
On considère un champ de force dont l'interaction avec la particule de charge $\ e$ se manifeste sous forme lagrangienne par $\ e.A^j.dx_j$

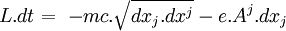
La définition de l'action relativiste infinitésimale d'un champ électromagnétique est $\ L.dt = \ -mc.\sqrt{dx_j.dx^j} - e.A^j.dx_j$ .

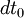
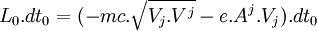
En factorisant par $\ dt_0$ un temps paramétrant le système, pas obligatoirement propre, on obtient : $L_0.dt_0 = ( -mc.\sqrt{V_j.V^j} - e.A^j.V_j).dt_0$

Les équations d'Euler-Lagrange relativistes

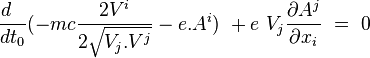
donnent : $\frac{d~~ }{dt_0} (-mc\frac{2V^i}{2\sqrt{V_j.V^j}}- e.A^i) \ + e\ V_j \frac{\partial A^j}{\partial x_i} \ = \ 0$

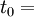
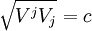
En prenant dès maintenant $\ t_0 =$ temps propre, on utilise l'égalité $\sqrt{V^jV_j} = c ~$ qui simplifie la dérivation

(mais on peut dériver avant si on veut plus de cohérence dans le suivi de la méthode), et on a :

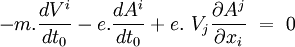
$-m. \frac{dV^i}{dt_0} - e.\frac{dA^i}{dt_0} + e. \ V_j \frac{\partial A^j}{\partial x_i} \ = \ 0$

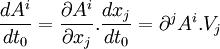
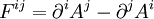
Sachant que $\frac{dA^i}{dt_0} = \frac{\partial A^i}{\partial x_j}. \frac{dx_j}{dt_0} = \partial^j A^i.V_j \ \$ et en posant $F^{ij} = \partial^i A^j - \partial^j A^i$ tenseur champ électromagnétique,

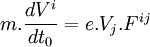
on obtient l'équation du mouvement : $m. \frac{dV^i}{dt_0} = e.V_j.F^{ij}$

On retrouve le cas sans quadri-écriture en factorisant par $\ c.dt$ le temps du référentiel, en prenant

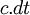
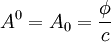
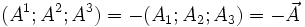
$\ A^0 = A_0 = \frac{\phi}{c}~~$ et $(A^1;A^2;A^3) = - (A_1;A_2;A_3) = - \vec{A}$ .

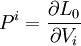
On se rappelle que la quadri-impulsion, comme l'impulsion, est définie par $P^i = \frac{\partial L_0}{\partial V_i}$

D'où :

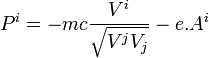
Pour

i = 0

, on obtient :

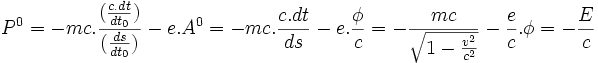
Pour

i = 1;2;3

, de manière similaire au cas i=0, on obtient :

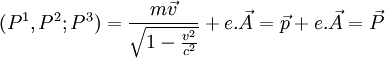
De manière similaire au cas d'un corps libre, la constante

par rapport au temps

est en fait la constante 0, et une petite manipulation permet d'en déduire l'égalité déjà vue

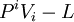
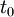
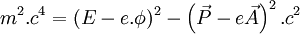
L'invariance de jauge du potentiel et du tenseur électromagnétiques

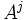
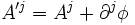
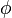
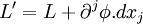
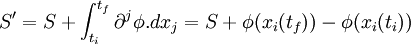
On remarque que si à la place du quadri-potentiel électromagnétique $\ A^j$ , on a le quadri-potentiel $\ A'^j = A^j + \partial^j \phi$ où $\ \phi$ est une fonction quelconque des coordonnées, alors le lagrangien devient $L' = L + \partial^j \phi.dx_j$ et l'action $S' = S + \int^{t_f}_{t_i}\partial^j \phi.dx_j = S + \phi (x_i(t_f)) - \phi (x_i(t_i))$

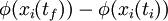
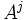
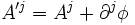
En appliquant la méthode variationnelle qui fait varier le chemin en gardant les extrémités fixes, le terme $\ \phi (x_i(t_f)) - \phi (x_i(t_i))$ est éliminé. Donc les deux potentiels $\ A^j$ et $\ A'^j = A^j + \partial^j \phi$ donnent les mêmes équations du mouvement : on appelle cela l'« invariance de jauge ».

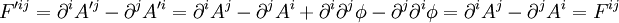
On constate d'ailleurs que dans les équations du mouvement, le tenseur électromagnétique, terme représentant l'influence du champ électromagnétique, est bien invariant de jauge : $F'^{ij} = \partial^i A'^j - \partial^j A'^i = \partial^i A^j - \partial^j A^i + \partial^i \partial^j \phi- \partial^j \partial^i \phi = \partial^i A^j - \partial^j A^i = F^{ij}$

par le théorème de Schwarz : $\partial^i \partial^j = \partial^j \partial^i$ .

Avec ou sans quadri-écriture

Cas d'un corps libre

- Introduction - Avec ou sans quadri-écriture - Cas d'un corps dans un champ électromagnétique - Cas d'un corps libre - Cas d'un champ « de force »

Un trou noir solitaire identifié pour la première fois 🔭

Comment nos médicaments changent le comportement des poissons 🐟

Cette nouvelle théorie unifie-t-elle enfin électromagnétisme et gravité ? ⚡

Découverte d'un vecteur de la maladie du sommeil 💤

La face cachée de la Lune révèle une étrangeté 🌓

Piéger le CO2 sous terre indéfiniment, c'est possible ! 🌍

La plus lointaine cousine de la Voie Lactée jamais observée 🌀

Ce codex médiéval cache un secret dans son bois 🔍

Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋

Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️

Des singularités temporelles dans l'Univers ? 🕰️

Des fossiles de dinosaures mieux datés 🦖

Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭

Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆

Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜

Le rôle méconnu de la décharge dans l'usure des batteries 🔋

La fonte des glaces déplace les pôles: quelles conséquences ? 🌍

L'appareil photo de votre smartphone peut détecter l'antimatière 📱

Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐

Un mosasaure géant découvert dans le Mississippi 🦕

Problème, les galaxies meurent plus tôt que prévu 🌀

Ce lien entre cannabis et troubles psychotiques 🧠

Une révolution dans le refroidissement des puces électroniques ? 🔥

Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀

Lucy survole un astéroïde en forme de cacahuète 🚀

Découverte du fossile d'un dinosaure géant méconnu 🦕

Mars avait-elle un champ magnétique unilatéral ? 🔍

Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇

Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁

L'électroluminescence du graphène, une découverte inattendue ! 💡

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Page générée en 0.131 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise