Problèmes de Hilbert - Définition

Seizième problème

Ce problème comporte deux parties. La première concerne le nombre de branches réelles (ovales) d'une courbe algébrique, et leur disposition ; de nombreux résultats modernes (Petrovskii, Thom, Arnold) apportent des informations à leur sujet.

La seconde partie du problème pose la question du nombre maximal et de la position mutuelle des cycles limites de Poincaré (orbites périodiques isolées) pour une équation différentielle polynomiale plane de degré donné ; cette question est encore ouverte.

Dix-neuvième problème

Prouver que le calcul des variations est toujours nécessairement analytique.

Résolu par Bernstein et Radó (en) en 1929.

Dix-huitième problème

Construire un espace euclidien avec des polyèdres congruents.

Le problème comporte trois parties.

• Premièrement, montrer qu'il n'existe à isomorphisme près qu'un nombre fini de groupes discrets d'isométries de admettant un domaine fondamental compact ; cette question fut résolue par Ludwig Bieberbach en 1910.
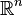
• Deuxièmement, la question de l'existence de polyèdres qui ne sont pas des groupes fondamentaux, mais qui peuvent cependant paver l'espace ; de tels polyèdres furent construits par Reinhardt et Heesch dans les années trente.
• Troisièmement, ce problème comporte aussi la fameuse conjecture de Kepler sur l'empilement des sphères dans l'espace, résolue en 1998 par Thomas Hales.

Vingt-et-unième problème

Prouver que toute représentation complexe de dimension finie peut s'obtenir par action de monodromie sur une équation différentielle de Fuchs.

Résolu par Helmut Rörl en 1957.

Vingtième problème

Étudier la solution générale des problèmes de valeur limite.

Vingt-troisième problème

Développer une méthode générale de résolution dans le calcul des variations.

Vingt-deuxième problème

Uniformiser des courbes analytiques au moyen de fonctions automorphes.

Résolu par Koebe et Henri Poincaré en 1907.