Problèmes de Hilbert - Définition

Introduction

Lors du deuxième congrès international des mathématiciens tenu à Paris en 1900, David Hilbert présenta une liste de problèmes qui tenaient jusqu'alors les mathématiciens en échec. Ces problèmes devaient, selon Hilbert, marquer le cours des mathématiques du XX^e siècle, et l'on peut dire aujourd'hui que cela a été grandement le cas. La liste définitive fut publiée après la tenue du congrès et est aujourd'hui familièrement appelée problèmes de Hilbert.

Les sections suivantes présentent brièvement chaque problème.

Premier problème

Tout sous-ensemble infini des réels peut être mis en bijection avec l'ensemble des entiers naturels ou avec l'ensemble des réels lui-même.

Il s'agit de l'hypothèse du continu de Cantor. Ce résultat aurait eu pour conséquence que le cardinal infini qui suit immédiatement le dénombrable, est celui du continu.

Kurt Gödel a montré en 1938 que l'on ne pouvait pas démontrer la négation de l'hypothèse du continu dans la théorie des ensembles ZFC, et Paul Cohen en 1963 que l'on ne pouvait pas non plus la démontrer (dans cette même théorie) : on dit que cette conjecture est indécidable dans la théorie ZFC (ou indépendante de celle-ci).

Comme on considère que la théorie ZFC permet largement de formaliser le développement des mathématiques jusqu'à aujourd'hui, la question peut paraître réglée. Cependant, l'existence d'axiomes supplémentaires « naturels » qui s'ajouteraient à la théorie ZFC et pourraient décider l'hypothèse du continu reste un domaine de recherche.

Troisième problème

Étant donnés deux polyèdres d'égal volume, peut-on découper le premier polyèdre en des polyèdres et les rassembler pour former le second polyèdre ?

Max Dehn, élève de Hilbert, montra que non, en 1902, en démontrant qu'il était impossible de diviser un cube et un tétraèdre régulier de même volume en un nombre fini de polyèdres deux à deux identiques. Malgré tout, le paradoxe de Banach-Tarski constitue un résultat positif pour cette question si l'on n'exige pas que les morceaux intermédiaires soient des polyèdres et surtout si l'on suppose l'axiome du choix.

Deuxième problème

Peut-on prouver la cohérence de l'arithmétique ? En d'autres termes, peut-on démontrer que les axiomes de l'arithmétique ne sont pas contradictoires ?

Gödel montra en 1931, via son théorème d'incomplétude, que cela ne pouvait être démontré sans sortir de l'arithmétique. Gerhard Gentzen, cependant, donna, en 1936, une réponse affirmative au moyen d'une récurrence transfinie.

Cinquième problème

Démontrer que les groupes de Lie sont nécessairement différentiables.

Le théorème de Gleason-Montgomery-Zippin en 1953 y répondit par l'affirmative.

Quatrième problème

Définir toutes les géométries dont la plus courte distance entre deux points est un segment de droite.

La géométrie différentielle a permis de répondre en partie à ce problème, bien que l'on ne puisse pas à proprement parler de réponse ferme.

Septième problème

Démontrer la transcendance des nombres a^b, avec a algébrique différent de 0 et 1, et b algébrique irrationnel (par exemple .

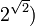
Les travaux de Gelfond et de Schneider ont permis de résoudre ce problème (voir Théorème de Gelfond-Schneider). Ce résultat a été généralisé par Baker (voir Théorème de Baker).

Sixième problème

L'axiomatisation, fondée sur le modèle mathématique, de la physique.

Du fait de l'apparition de la théorie de la relativité et de la mécanique quantique, le problème fut vite obsolète. Malgré tout, la physique théorique et les mathématiques ne cessent de se rapprocher. En axiomatisant la théorie des probabilités, Kolmogorov a résolu en partie ce problème.