Problèmes de Hilbert - Définition
La liste des auteurs de cet article est disponible ici.
Neuvième problème
- Établir une loi de réciprocité dans les corps de nombres algébriques.
Une réponse à ce problème est apportée par la loi de réciprocité d'Artin, démontrée par celui-ci en 1927.Ce théorème enrichit la connaissance de la théorie des corps de classes, dont le développement fut facilité par l'introduction des idèles par Chevalley en 1936.
Huitième problème
- Démontrer l'hypothèse de Riemann.
Malgré les progrès faits notamment par Deligne qui démontra les conjectures de Weil, et reçut pour cela la médaille Fields en 1978, on est encore loin d'avoir résolu ce problème, qui s'annonce comme celui du XXIe siècle.
Onzième problème
- Classer les formes quadratiques à coefficients dans les anneaux d'entiers algébriques.
Le théorème de Hasse-Minkowski résout le problème sur

Dixième problème
- Trouver un algorithme déterminant si une équation diophantienne a des solutions.
Il fallut attendre les travaux de Church et Turing en 1930 pour définir rigoureusement la notion d'algorithme. En 1970, Yuri Matijasevic, établissant une équivalence entre les ensembles récursivement énumérables et les ensembles diophantiens, a établi qu'un tel algorithme ne pouvait pas exister.
Treizième problème
- Montrer l'impossibilité de résoudre les équations du septième degré au moyen de fonctions de seulement deux variables.
Plus généralement, il s'agit d'étudier les fonctions continues (et, en fait, les fonctions continues de trois variables) qui ne peuvent pas s'exprimer par composition à partir de fonctions continues de deux variables. En 1954, Kolmogorov et son élève Vladimir Arnold ont montré que cette classe était vide : il existe n(2n + 1) fonctions continues universelles Φij (de [0;1] dans [0;1]) telles que pour toute fonction continue
![f:[0;1]^n \to [0;1]](https://static.techno-science.net/illustration/Definitions/autres/f/ff49e287250297e479a4deb2e62a514e_6a468978aa9b36b0c3fbb118ad225c68.png)
![g_j :[0;1] \to [0;1]](https://static.techno-science.net/illustration/Definitions/autres/8/88b87551bcd4949ecd397a3943c35a15_a7e25cc5dddb5da8426ad25c290f4e47.png)
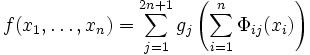
Douzième problème
- Prolonger le théorème de Kronecker sur les corps non-abéliens.
Quinzième problème
- Mettre en place les bases du calcul énumératif de Hermann Schubert.
Il s'agit là de rendre rigoureux certains calculs sur les objets « en position générale » en théorie de l'intersection, et en particulier le « principe de conservation des nombres ». Ce problème a donné naissance aux théories de la multiplicité de Samuel et Grothendieck.
Résolu par van der Waerden en 1930.
Quatorzième problème
- Prouver le caractère fini de certains systèmes complets des fonctions.
Le problème est le suivant : on considère un corps k et un sous-corps K de
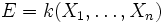
![R = k[X_1 , \dots, X_n ]](https://static.techno-science.net/illustration/Definitions/autres/7/7e3151a34a4bb6278e53303fb36457d6_5f9c0b08eb098520cc145fb1ba327ec9.png)
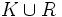
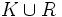
Nagata donna en 1959 un contre-exemple qui montra la fausseté de la conjecture.
Dix-septième problème
- Montrer qu'une fonction rationnelle positive peut s'écrire sous la forme de somme de carrés de fonctions rationnelles.
Résolu par Emil Artin en 1927. Une démonstration par la théorie des modèles a été trouvée par le logicien Abraham Robinson.

















































