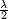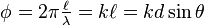Réseaux d'antennes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un réseau d'antennes est un ensemble d'antennes séparées et alimentées de façon synchrone. C'est-à-dire que le déphasage du courant entre chaque paire d'antennes est fixe. Nous verrons plus loin qu'un réseau peut comporter des éléments non alimentés directement par une source (éléments parasites) mais qui sont alimentés par le champ produit par le reste des éléments (c'est la cas des antennes Yagi-Uda). Le champ électromagnétique produit par un réseau d'antennes est la somme vectorielle des champs produits par chacun des éléments. En choisissant convenablement l'espacement entre les éléments et la phase du courant qui circule dans chacun, on peut modifier la directivité du réseau grâce à l'interférence constructive dans certaines directions et à l'interférence destructive dans d'autres directions.
Radiation d'une paire d'antennes
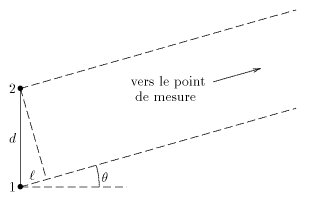
Soient deux antennes identiques séparées d'une distance

Calculons le champ électrique produit par cette paire d'antennes à une distance très grande des antennes. C’est-à-dire que


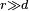


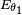
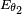
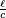
Ici,
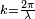
Comme les deux champs sont parallèles, la somme vectorielle se réduit a additionner les amplitudes, mais en tenant compte du déphasage :
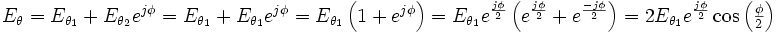
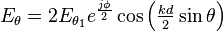
Comme la phase du champ électrique reçu ne pressente aucun intérêt et que seule l'amplitude est importante, seul le module de ce nombre nous intéresse :
Il est facile de constater que pour
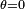
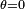
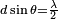

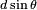
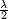
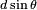
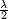

Il ne faut pas oublier, non plus, que l'émission est symétrique autour de l'axe qui passe par les antennes.
Les antennes ont un diagramme d'émission propre. Le champ que nous avons calculé ne tient compte que de l'aspect interférence entre les deux ondes émisse par chacune des antennes. Dans le calcul et la visualisation du résultat final il faut tenir aussi compte du diagramme de radiation des antennes. Par exemple, le calcul que nous venons de faire peut donner un maximum pour
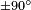
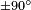
Voici un exemple formé par deux antennes dipôle verticales
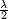
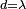
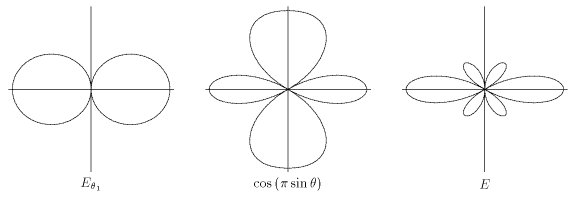
À gauche nous avons dessiné le digramme de radiation d'un dipôle