Champ électrique - Définition

Introduction

Représentation du champ électrique en quelques points de l'espace dû à une charge élémentaire postive.

Champ électrique associé à son propagateur qu'est le photon.

Michael Faraday introduisit la notion de champ électrique.

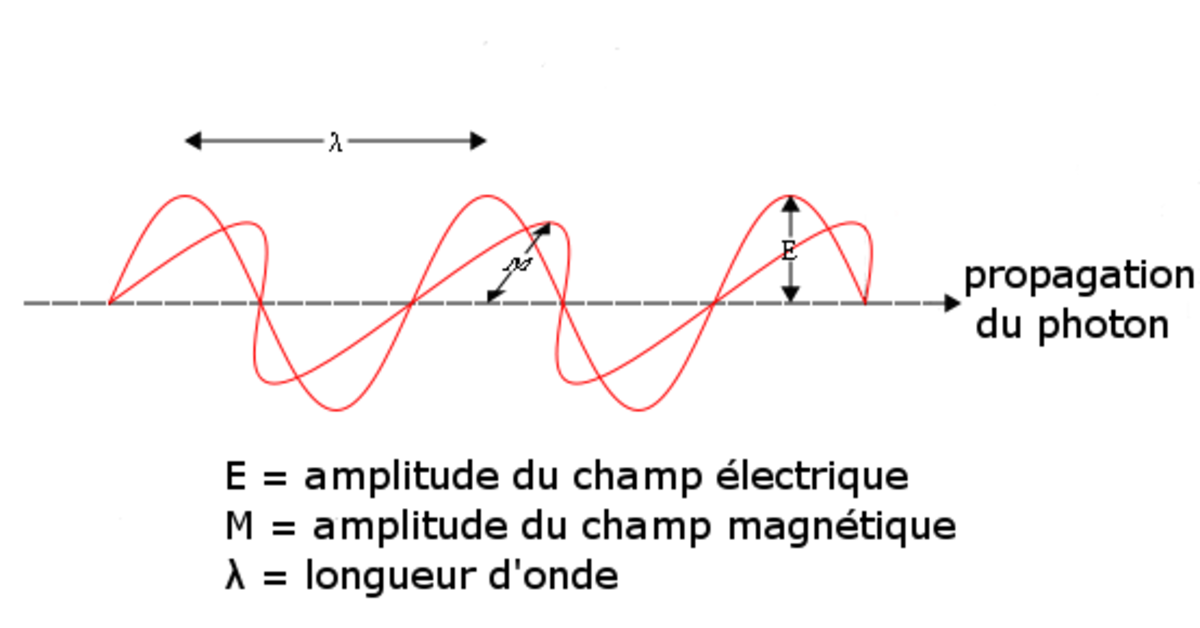
En physique, on désigne par champ électrique un champ créé par des particules électriquement chargées. Un tel champ permet de déterminer en tout point de l'espace la force électrique exercée à distance par ces charges. Dans le cas de charges fixes dans le référentiel d'étude, le champ électrique est appelé champ électrostatique. Lorsque les charges sont en mouvement dans ce référentiel, il faut y ajouter un champ électrique induit dû aux déplacements des charges pour obtenir le champ électrique complet.

Description sommaire

Illustration des vecteurs de champ électrique (en bleu) entre une charge positive (en rouge) et une charge négative (en vert)

Diagrammes de lignes de champs entre deux charges de mêmes signe (gauche) et deux charges de signe opposé (droite). La force qui en résulte est répulsive pour le premier et attractive pour le deuxième.

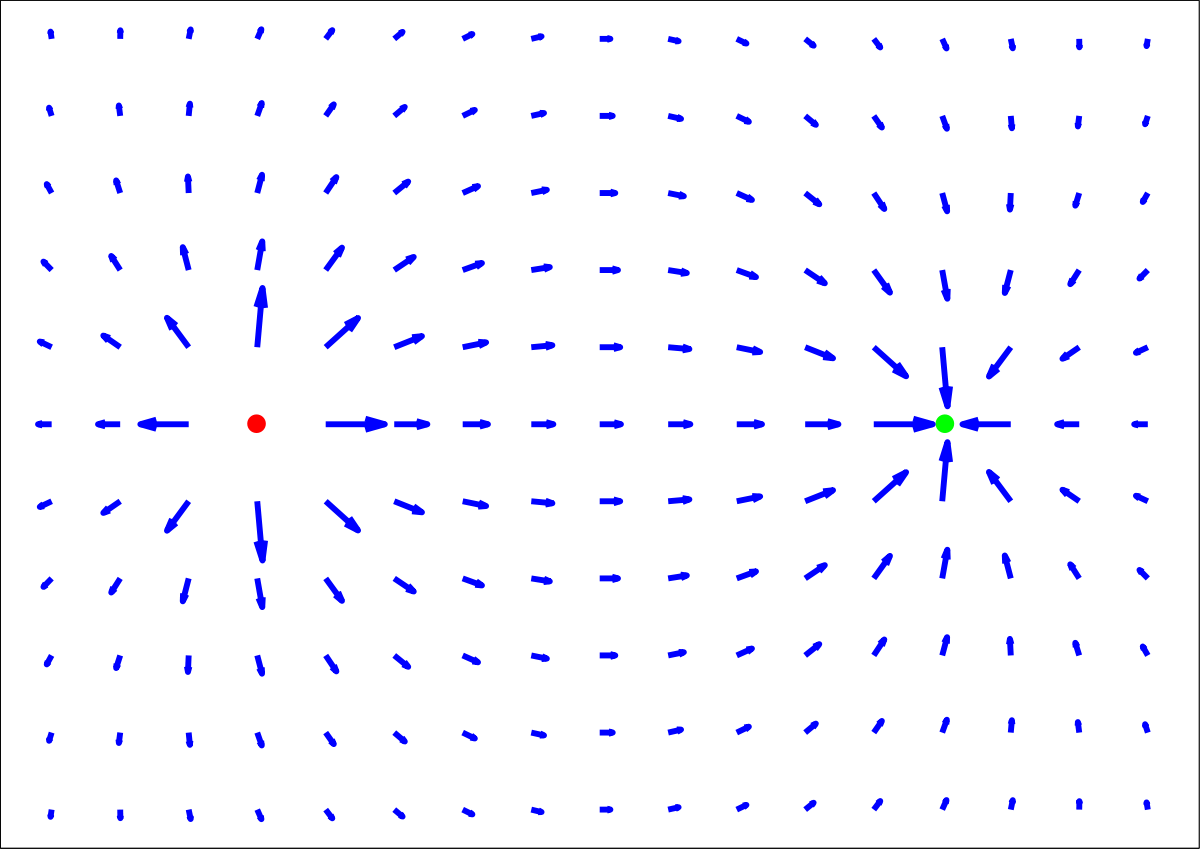
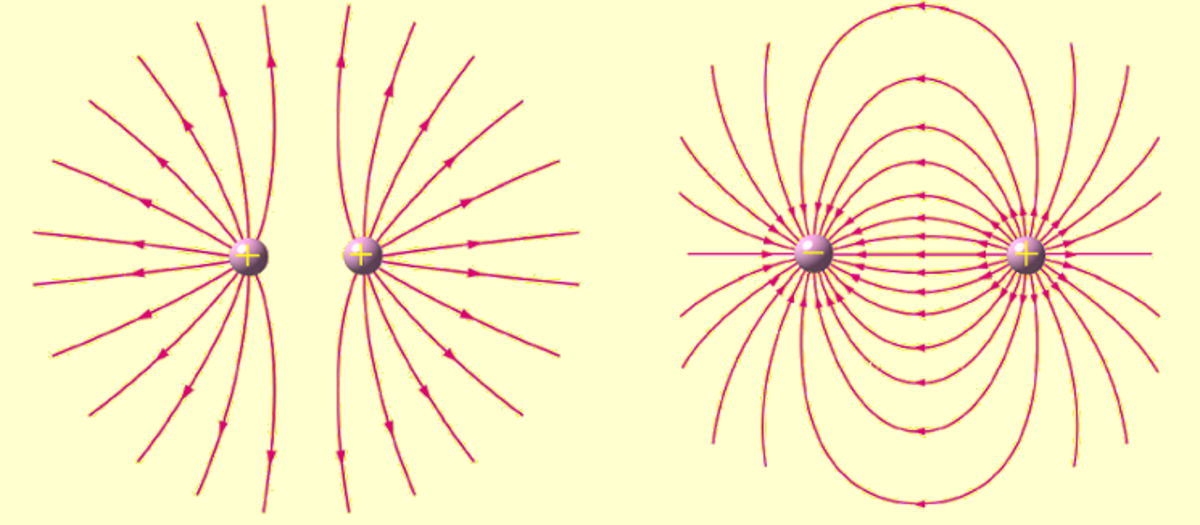
Le champ électrique est le champ vectoriel qui résulterait de l'action à distance de particules électriquement chargées sur une particule test de charge unité au repos dans le référentiel d'étude. C'est donc la force subie par la particule au repos divisée par la charge de cette particule. Il s'agit d'un champ vectoriel qui à tout point de l'espace associe une direction, un sens, et une grandeur (amplitude). La norme de ce vecteur s'exprime en volt par mètre (V/m) ou en newton par coulomb (N/C) dans le système international d'unités.

La portée du champ électrique est théoriquement infinie, ses valeurs en tout point dépendant de la distribution de charges ou de la nature des matériaux remplissant l'espace. Noté généralement par , sa propagation est régie par les équations de Maxwell. Historiquement il fut introduit au milieu du XIX^e siècle par Michael Faraday pour expliquer dans ses expériences certaines actions à distance, cette interaction est aujourd'hui reconnue comme portée par le photon.

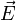
Associé au champ magnétique, il forme le champ électromagnétique qui est à la base d'une des quatre interactions fondamentales de l'univers : l'interaction électromagnétique.

Cas de particules en mouvement

Lorsque les particules chargées qui créent le champ sont en mouvement dans le référentiel d'étude il convient d'ajouter au champ électrostatique un champ électrique induit E_i dû au mouvement de ces charges. Ce champ électrique induit est directement relié au champ magnétique B créé par ces charges en mouvement par l'intermédiaire du potentiel vecteur A

où

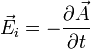
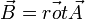
le champ électrique total est alors

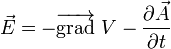
C'est ce champ qu'il faut prendre en compte dans le cas général pour exprimer la force de Lorentz.

Champ électrostatique

Lorsque les charges qui créent le champ sont au repos dans le référentiel d'étude on parle de champ électrostatique. Ce champ est alors directement déduit de l'expression de la loi de Coulomb (ou interaction électrostatique).

Expression du champ électrostatique créé par une charge ponctuelle Q

L'expression du champ électrique est directement issue de l'expression de la force électrostatique donnée par la loi de Coulomb, et dépend du point de l'espace où l'on se place. Dans le cas où l'on ne considère qu'une seule particule chargée Q comme source du champ, celui-ci est orienté des sources vers le point considéré et a pour valeur où Q désigne la charge électrique, la permittivité du milieu et la distance entre la source et le point considéré.

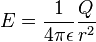
Mesure effective

Pour mesurer l'influence des sources, on peut utiliser une autre particule, elle aussi chargée électriquement avec une charge (l'unité SI de charge électrique est le Coulomb, noté C), qui sert de particule test. Alors si on appelle le champ électrique créé par les sources à l'endroit où se trouve la charge test (on va donner plus bas les détails sur la façon de déterminer ) cette dernière subit une force électrique donnée par

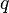
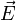
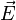
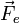
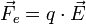
Relation avec le potentiel électrostatique

Le champ électrostatique est directement relié au potentiel électrique V par la formule :

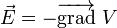
on dit que le champ électrique dérive du potentiel électrique par l'intermédiaire d'un gradient.

Effets

Le champ électrique peut ainsi mettre en mouvement des particules chargées. À la différence du champ magnétique il est capable de les accélérer. Bien que négligeable à une grande échelle devant l'interaction gravitationnelle car la matière est globalement neutre électriquement (c'est le cas de la majorité des systèmes planétaires), le champ électrique a un effet prépondérant à des échelles microscopiques, et est utilisé pour l'étude de la matière dans les accélérateurs de particules.

Un champ électrique peut être créé relativement facilement entre deux plaques de condensateur, c’est-à-dire deux plaques dont la tension entre les deux est non nulle. Voir plus bas pour un calcul détaillé.

Analogie avec le champ gravitationnel

Il existe une analogie forte entre le champ électrique et le champ gravitationnel : l'expression du champ et du potentiel ne diffèrent que d'une constante, et les principaux théorèmes de calcul (comme celui de superposition ou de Gauss) s'appliquent. La principale différence tient au fait que le champ électrique peut être attractif (entre deux charges de signe opposé) ou répulsif (entre deux charges de même signe) alors que le champ gravitationnel est purement attractif.