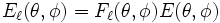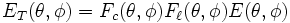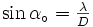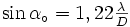Réseaux d'antennes - Définition
La liste des auteurs de cet article est disponible ici.
Problèmes pratiques propres aux réseaux d'antennes
Dans tout ce qui a été dit précédemment, nous avons gardé sous silence l'interaction entre antennes.
L'interaction entre éléments individuels induit des courants dans les autres éléments ce qui modifie l'impédance de l'élément, ce qui peut modifier la phase du courant d'alimentation. Ceci fait que fixer la phase de chaque élément quand les éléments interagissent est extrêmement compliqué. Une façon de contourner le problème est d'alimenter un seul élément. De cette façon la phase du courant des autres éléments est fixée par la seule géométrie du réseau. C'est la solution utilisée dans les antennes Yagi-Uda. Une autre façon d'éviter les interactions est de choisir le type d'antenne individuelle et sa disposition. Ainsi, si on utilise des antennes dipolaires, on peut les disposer alignées, car ces antennes n'émettent pas dans le sens de leur longueur. Une autre possibilité est celle d'utiliser des antennes individuelles qui ne rayonnent pas dans la direction des autres antennes du réseau. C'est la solution utilisée dans les "phased arrays".
Réseau bidimensionnel d'antennes
Les réseaux bidimensionnels d'antennes furent très utilisés il y a quelques décades pour faire des émissions directionnelles dirigées horizontalement en ondes courtes. Ces communications servaient à communiquer avec d'autres continents ou avec des navires en mer. Bien entendu, avec l'utilisation des satellites de communication, la communication commerciale par des ondes courtes et les énormes réseaux d'antennes nécessaires sont disparus et nous n'en parlerons pas.
Maintenant un autre type de réseau bidimensionnel d'antennes est utilisée. Ce sont les antennes utilisées surtout dans les radars à balayage (phased arrays en anglais). Comme nous verrons, ce type d'antenne permet d'orienter le faisceau du radar sans déplacer mécaniquement l'antenne.
Les réseaux bidimensionnels d'antennes actuelles sont formés par quelques milliers d'émetteurs individuels disposés en réseau bidimensionnel carré, rectangulaire ou, plus souvent, hexagonal. Pour comprendre le principe de fonctionnement, imaginez un réseau d'émetteurs formant un réseau carré sur l'écran de votre ordinateur.

Si vous êtes placé loin de l'écran, et que tous les émetteurs sont alimentés en phase, pour recevoir toutes les émissions en phase vous devez vous placer dans la perpendiculaire à l'écran qui passe par le réseau. Maintenant changeons la phase de l'alimentation des émetteurs de façon que chaque émetteur soit en avance de phase par rapport à son voisin de droite (la vôtre). Pour recevoir tous les émetteurs en phase et ainsi rester sur l'axe du faisceau vous devrez vous déplacer vers vôtre droite, pour vous éloigner des émetteurs qui émettent avec avance de phase.
De la même façon, si nous voulons que le faisceau principal aille vers le haut, nous devons avancer la phase de chaque émetteur par rapport à son voisin d'en haut.
Un réseau bidimensionnel peut être considéré comme un réseau linéaire dont les émetteurs sont des réseaux linéaires à émission transversale.
Ainsi, si chaque émetteur individuel a un diagramme d'émission du type
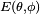

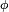
Où
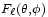
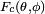
Nous n'irons pas plus loin dans le calcul des facteurs
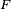
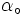
Où

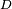
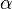
Cette fois,
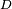
Ces formules sont valables quand le faisceau est perpendiculaire au réseau. Si les déphasages donnés font que le faisceau est incliné d'un angle

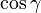
L'intérêt de ce type de réseau est que, si on équipe chacun des quelques milliers d'émetteurs d'un dispositif individuel qui retarde l'émission (et la réception), on peut changer la direction dans laquelle "tire" l'antenne en quelques microsecondes à la place de secondes ou dixièmes de secondes nécessaires pour orienter mécaniquement une parabole. Évidemment, le retard de chaque dispositif est calculé et contrôlé par ordinateur. Ceci permet au radar (militaire, bien sur) de surveiller et traiter plusieurs cibles simultanément. Les utilisations sont surtout militaires : radars d'avions et navires militaires et des radars de systèmes anti-missiles utilisées dans les versions actuels de la La Guerre des étoiles. Au moins une application civile utilise ce type d'antenne. Il s'agit du réseau de téléphone satellite Iridium. Les antennes de ces satellites concentrent l'émission et réception dans une petite zone sous le satellite. Celui-ci balaye la petite zone sur une étendue beaucoup plus grande plusieurs milliers de fois par seconde.
Un autre intérêt de ce type d'antenne est que, comme il y a des milliers d'émetteurs, chacun n'émet que quelques dix-millièmes de la puissance totale, ce qui fait que les circuits retardateurs travaillent à puissance relativement réduite.
Pour calculer le retard à donner à chaque émetteur, il faut calculer la différence de chemin à parcourir entre les signaux de l'émetteur donné et celles de l'émetteur de référence. Cette distance est la projection du segment qui relie les deux émetteurs sur la droite dirigée vers la direction souhaitée du faisceau. Pour calculer cette projection on peut faire le produit scalaire du vecteur qui va de l'émetteur donné à l'émetteur de référence, par le vecteur unitaire parallèle à la direction souhaitée.