Interférence - Définition

Introduction

En mécanique ondulatoire, on parle d'interférences lorsque deux ondes de même type se rencontrent et interagissent l'une avec l'autre. Ce phénomène apparaît souvent en optique avec les ondes lumineuses, mais il s'obtient également avec des ondes électromagnétiques d'autres longueurs d'onde, ou avec d'autres types d'ondes comme les ondes sonores.

Définition

Une onde se modélise par une fonction , étant la position dans l'espace (vecteur) et t étant le temps.

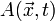
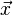
Lorsque l'on a deux sources distinctes, deux émetteurs, créant deux ondes A₁ et A₂, en un point donné, l'amplitude de A sera

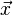
En physique, on considère classiquement deux phénomènes « idéaux » qui se produisent lorsqu'on mélange deux ondes sinusoïdales :

• l'interférence quand les deux ondes ont la même fréquence
• le battement quand les fréquences sont légèrement différentes.

Cette approche est justifiée par :

• le fait que toute fonction continue et périodique peut se décomposer en une somme de fonctions sinusoïdales (séries de Fourier) ;
• lorsque les fréquences sont très différentes, le résultat est bien plus simple.

Ondes sinusoïdales

Ondes de même fréquence déphasées (formule des interférences)

On considère deux ondes de même pulsation mais de phases différentes (cela peut être causé par un trajet multiple de l'onde dans sa propagation) d'expressions :

et

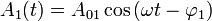
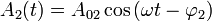
On cherche à mettre l'onde résultante sous la forme :

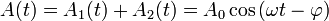
En développant, il vient :

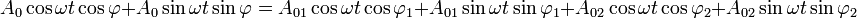
On doit donc résoudre simultanément :

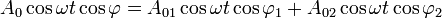
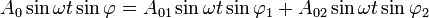
d'où :

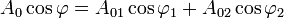
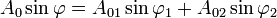
Calcul de l'amplitude de l'onde résultante

On obtient l'amplitude en élevant au carré et en sommant membre à membre les deux équations :

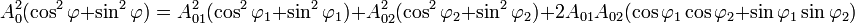
Et ainsi :

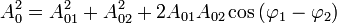
Si les ondes se superposent en phase ( ), on obtient :

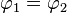
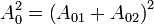
On parle d'interférence constructive, car la puissance résultante augmente.

Si les ondes se superposent en anti-phase ( ), on obtient :

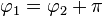
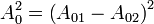
On parle d'interférence destructive, car la puissance résultante diminue.

Entre ces deux extrêmes, la puissance totale varie selon le cosinus de la différence des phases.

Calcul de la phase de l'onde résultante

On obtient la phase en rapportant membre à membre les deux équations précédentes :

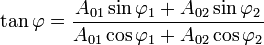
Finalement, l'expression de l'onde résultante se résume à :

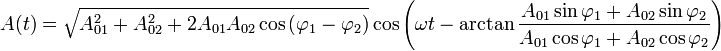
Ondes de fréquence proche (battements)

Voir l'article détaillé Battement.

Outils d'étude

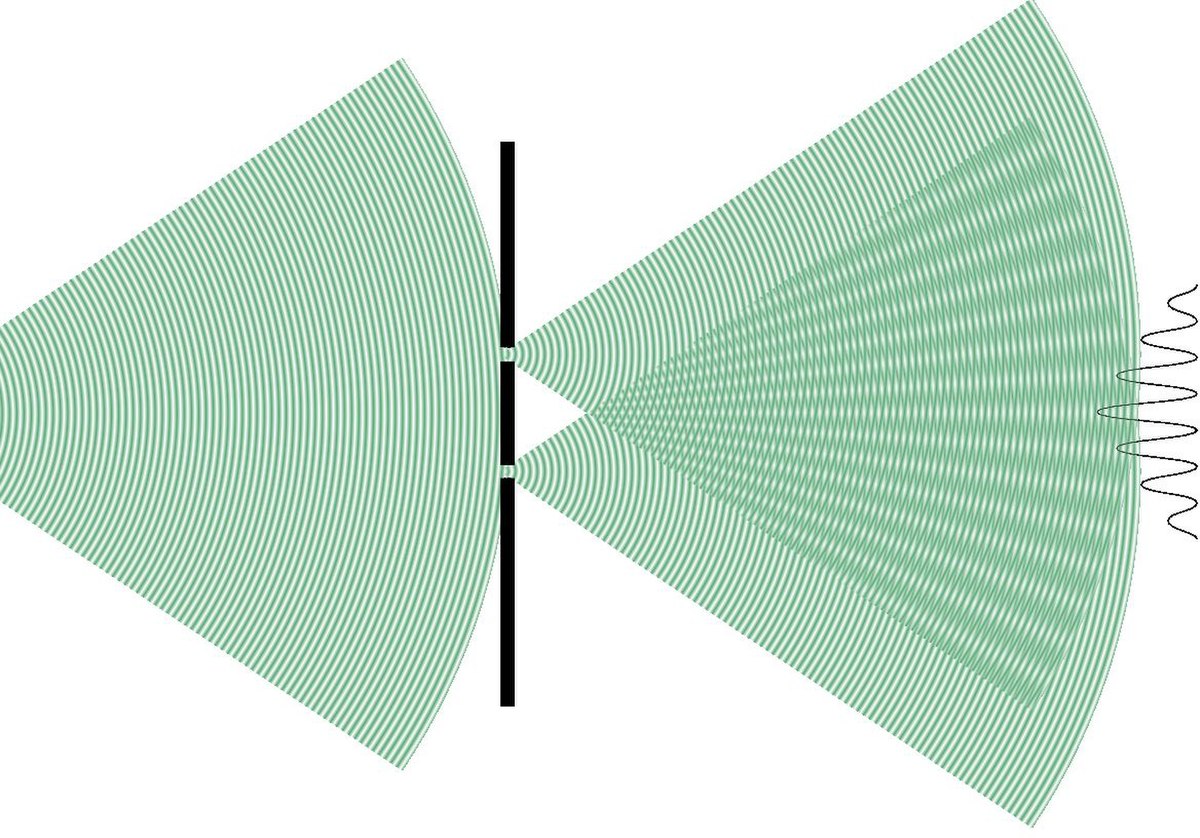
On utilise des interféromètres pour mesurer ou visualiser les interférences.

Citons les fentes de Young, l'interféromètre de Michelson, interféromètre à double miroir, l'interféromètre à lame transparente.

Interférences quantiques

Les interférences par des ondes (vagues, son, lumière) peuvent être obtenues par un raisonnement mathématique. Les particules élémentaires, comme les électrons ne devraient alors pas interférer de la même façon que ces ondes. Or d'après la mécanique quantique, on ne peut pas se restreindre à l'appellation de particule. En effet, celles-ci sont également des ondes. On devrait plutôt dire que ce ne sont ni des particules ni des ondes : ce sont des objets présentant des aspects parfois ondulatoires et parfois corpusculaires. Cette notion de dualité onde-corpuscule permet de comprendre que ce que l'on appelle souvent des particules peuvent aussi exhiber un comportement ondulatoire et donc présenter des interférences.

Ainsi, en 1961, C. Jönsson à Tübingen réalisait une expérience où un fil d'araignée métallisé séparant un faisceau d'électrons en deux produisait une interférence d'électrons. Dans la pratique, les électrons forment des impacts sur une plaque photographique, et la répartition de ces impacts présente des franges, de la même manière que pour la lumière.

Lorsqu'il a été possible de détecter les photons et les électrons individuellement, on a pu aussi montrer qu'il n'y a pas besoin d'une assemblée de particules pour faire des interférences : lorsqu'elles arrivent une par une, il y a également interférences. Cela permet de confirmer la célèbre affirmation de Dirac « chaque photon interfère seulement avec lui même » et l'expérience de pensée décrite par Feynman dans ses célèbres cours, où il se posait la question de savoir si la figure d'interférence apparaitrait même si les électrons arrivaient les uns après les autres devant deux fentes.

C'est en 1989 qu'une équipe de chercheurs de Hitachi (fabricant de microscopes électroniques) réussit à contrôler la production d'électrons et la détection un à un et à observer l'apparition dans le temps, électron après électron de la figure d'interférences. L'équipe d'Hitachi peut affirmer que, dans leur expérience, les électrons sont passés un à un comme indiqué dans l'expérience de pensée de Feynman. Ce que l'on observe est que les impacts successifs forment petit à petit les franges d'interférence.

Rappelons que Davisson et Thomson ont partagé le prix Nobel de physique de 1937 pour « la découverte de phénomènes d'interférences qui se produisent lorsque on expose des cristaux à un faisceau d'électrons » ce qui confirmait la thèse théorique de Louis de Broglie qui reçut le prix Nobel en 1929 pour sa découverte de l'aspect ondulatoire de l'électron.

Depuis, des interférences ont été observées avec des neutrons, des atomes et même des molécules comme le Buckminsterfullerène C₆₀. En effet avec un condensat de Bose-Einstein, il est possible de faire des interférences en coupant en deux et en observant les deux moitiés se mélanger. Ce qui est remarquable dans ces résultats, c'est que l'affirmation de Dirac semble s'appliquer à toute particule, qu'elle soit un boson ou un fermion.