Stellation - Définition
La liste des auteurs de cet article est disponible ici.
Les polygones étoilés
Une stellation d'un polygone régulier est un polygone étoilé ou un polygone composé.
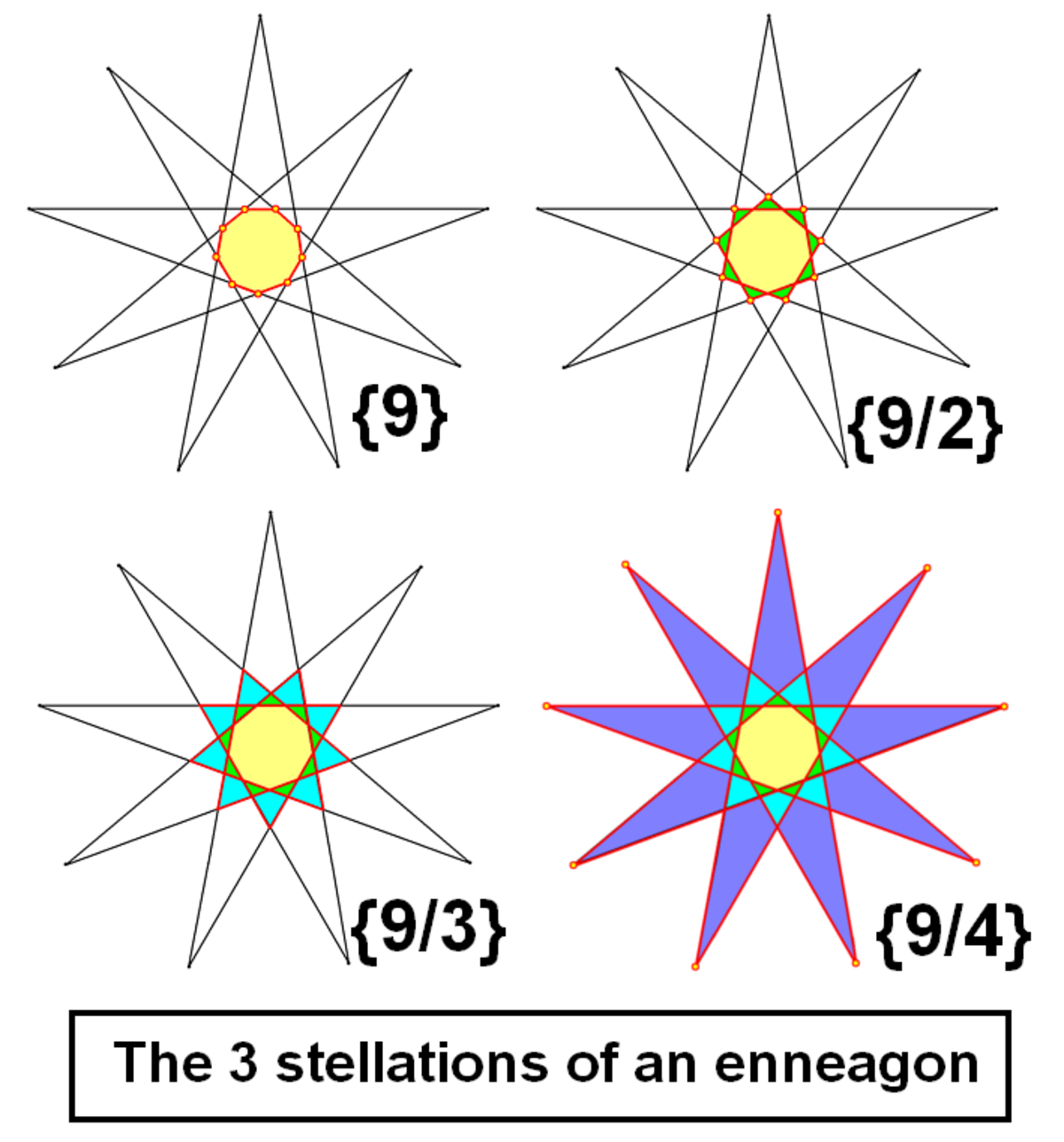
Il peut être représenté par le symbole {n/m}, où n est le nombre de sommets, et m, le pas utilisé dans la séquence des arêtes autour de lui. Si m est égal à un, c'est une stellation zéro, et un polygone régulier {n}. Et donc, la (m-1)ère stellation est {n/m}.
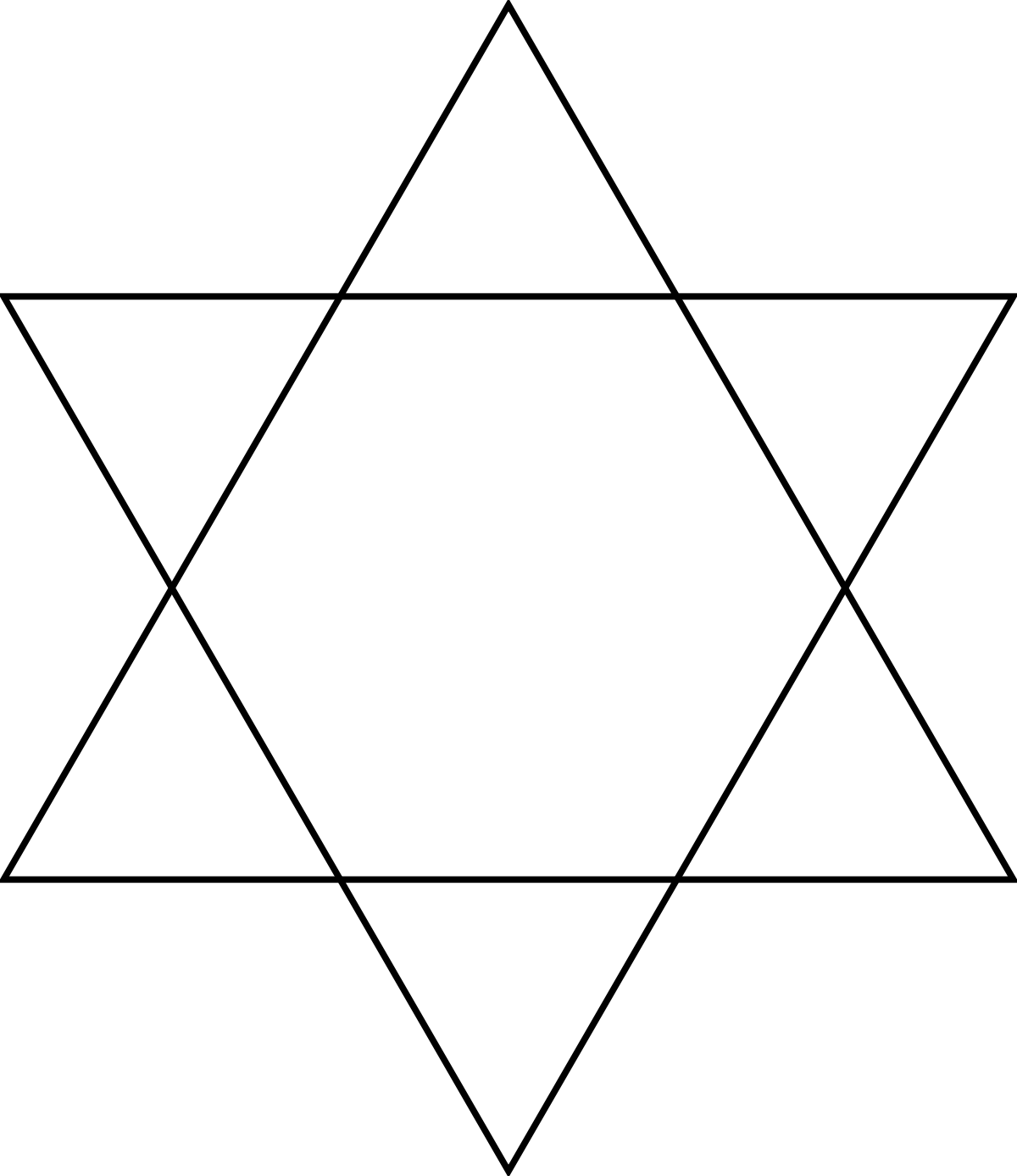
Un polygone composé apparaît si n et m ont un diviseur commun, et la stellation entière requiert de multiples chemins cycliques pour le compléter. Par exemple, un hexagramme {6/2} est fait par 2 triangles {3}, et {10/4} est fait par 2 pentagrammes {5/2}.
Un n-gone régulier possède (n-4)/2 stellations si n est pair, et (n-3)/2 stellations si n est impair.
Le pentagramme, {5/2}, est la seule stellation d'un pentagone |
L'hexagramme, {6/2}, la stellation d'un hexagone et un composé de deux triangles. |
L'ennéagone possède 3 formes ennéagrammiques : {9/2}, {9/3}, {9/4} avec {9/3} étant 3 triangles. |
| ||
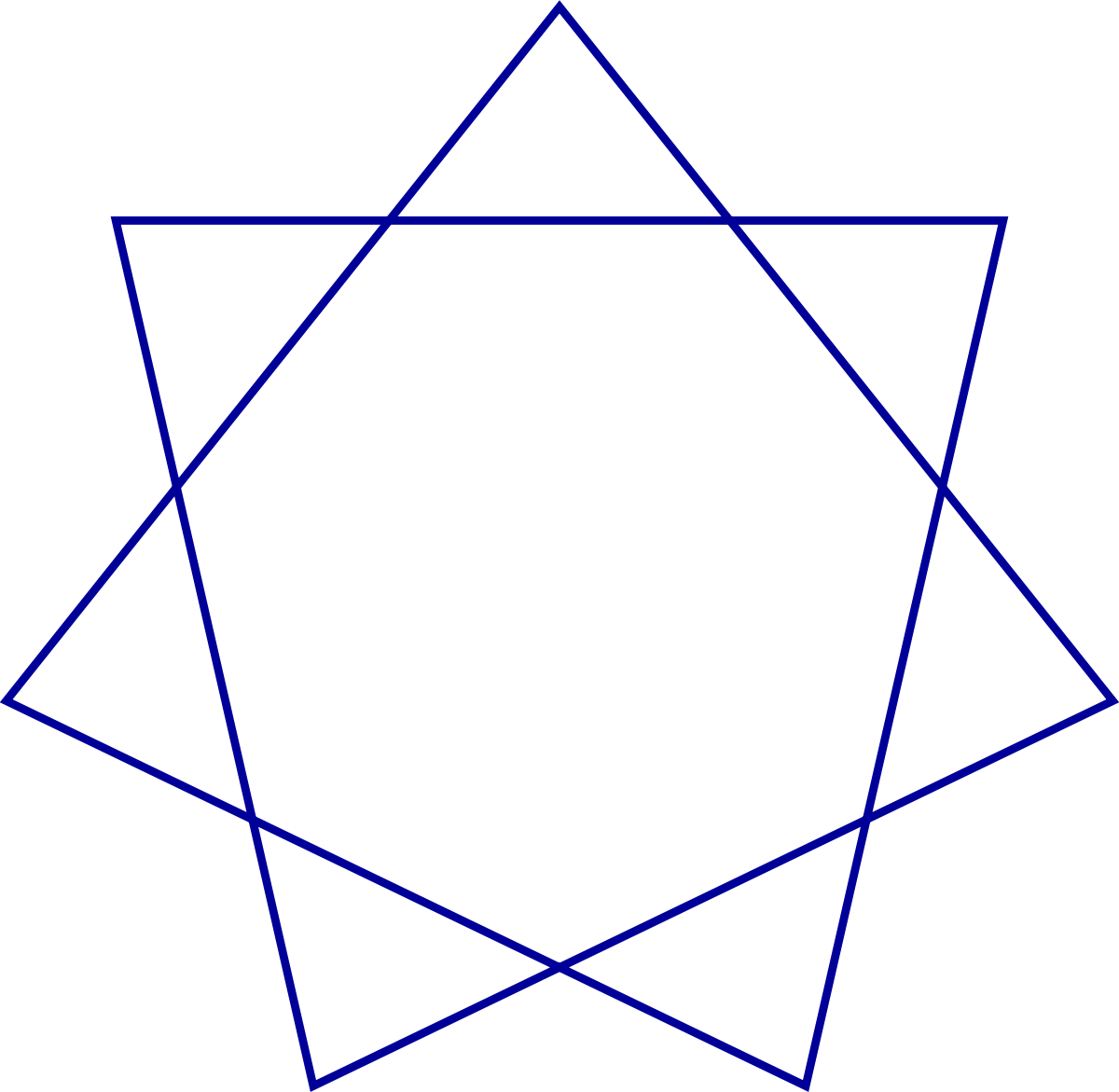
Comme l'heptagone, l'octogone possède aussi deux stellation octogrammiques, une, {8/3} étant un polygone étoilé, et l'autre, {8/2}, étant le composé de deux carrés.
Nomenclature des stellations
John Conway a conçu une terminologie pour les polygones, les polyèdres et les polychores étoilés (Coxeter 1974). Dans ce système, le procédé d'extension d'arête pour créer une nouvelle figure est appelé stellation, ce qui étend les faces est appelé élargissement (greatening) et ce qui étend les cellules est appelé agrandissement (aggrandizement) (ce dernier n'est pas appliqué aux polyèdres). Ceci permet un usage systématique de mots tels que 'étoilé', 'large' et 'grand' en concevant les noms pour les figures résultantes. Par exemple, Conway a proposé quelques variations mineures aux noms des polyèdres de Kepler-Poinsot.
