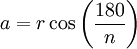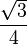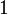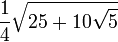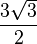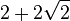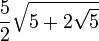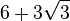Polygone régulier - Définition

Introduction

Pentagone convexe régulier

En géométrie, un polygone régulier est un polygone équilatéral (tous ses côtés ont la même longueur) dont, de plus, tous les angles ont même mesure. Un polygone régulier est soit un polygone convexe, soit un polygone étoilé (en).

Tous les polygones réguliers convexes d'un même nombre de côtés sont semblables.

Dans certains contextes, tous les polygones considérés seront convexes et réguliers. Dans de telles circonstances, il est d'usage de sous-entendre les deux épithètes « convexe régulier ». Par exemple, toutes les faces des polyèdres uniformes doivent être convexes et régulières et les faces seront décrites simplement en tant que triangle, carré, pentagone...

De tels polygones sont le support des nombres polygonaux.

Les multiples propriétés des polygones réguliers ont conduit à leur étude mathématique depuis l'Antiquité et à diverses interprétations symboliques, religieuses ou magiques.

Propriétés

Définition équivalente

Une définition équivalente de "polygone régulier" peut être formulée par rotation : si on se donne deux points O et A, un nombre entier n supérieur ou égal à 3, alors les images successives de A par des rotations de centre O et d'angles génèrent les sommets d'un polygone régulier à n côtés et centre O.

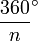
Vocabulaire

Apothème d'un hexagone régulier

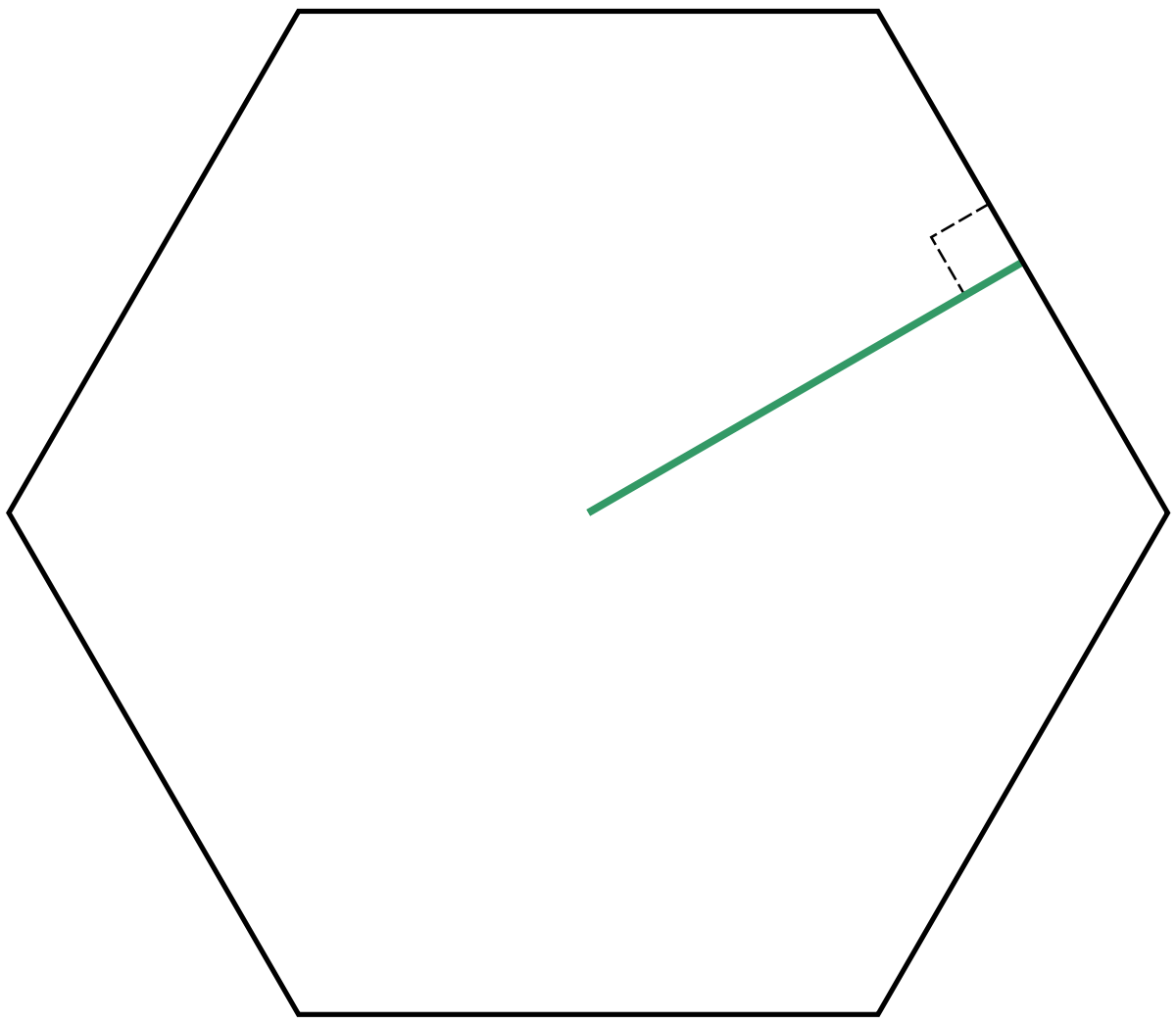
Tout polygone régulier est inscrit dans un cercle. Le centre et le rayon de ce cercle sont également appelés centre et rayon du polygone régulier. La distance entre le centre du polygone et chacun des côtés est l'apothème.

Comme les polygones convexes réguliers à n côtés sont semblables, la donnée d'une des trois longueurs (côté, rayon ou apothème) permet de connaître les deux autres et donc de caractériser le polygone.

Si on note a l'apothème, r le rayon et c la moitié du côté d'un polygone régulier à n côtés, ces longueurs sont liées par le théorème de Pythagore :

a² + c² = r²

et par les formules de trigonométrie (les angles étant exprimés en Degrés) suivantes :

Angles

Les angles au centre d'un polygone régulier à n côtés mesurent .

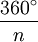
Chaque angle d'un polygone convexe régulier à n côtés a une mesure de degrés, ou encore radians ou tours.

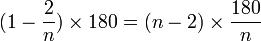
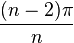
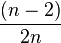
Aire et périmètre

Si t est la longueur d'une arête, l'aire a et le périmètre p d'un polygone convexe régulier à n côtés est donnée par la formule suivante :

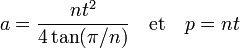
Si ρ désigne le rayon du polygone, c'est-à-dire la distance entre le centre et un sommet, on obtient :

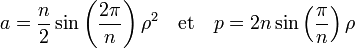
Cette aire est aussi égale à la moitié du périmètre multiplié par la longueur de l'apothème.

Si n est grand, les valeurs π/n et 2π/n deviennent petites, le sinus d'une petite valeur est proche de cette valeur. Plus la valeur est petite, plus la proximité est bonne, on en déduit que plus le nombre de côtés d'un polygone augmente, plus son périmètre et son aire se rapprochent de ceux d'un cercle de même rayon.

Les polygones convexes réguliers ont une propriété remarquable, connue depuis les grecs. Parmi tous les polygones de même nombre de côtés et de même périmètre, celui qui est convexe régulier possède la plus grande aire. Cette aire, toujours plus petite que celle du cercle de même rayon, s'en rapproche au fur et à mesure que n devient plus grand. Ces propriétés sont traitées dans l'article Isopérimétrie.

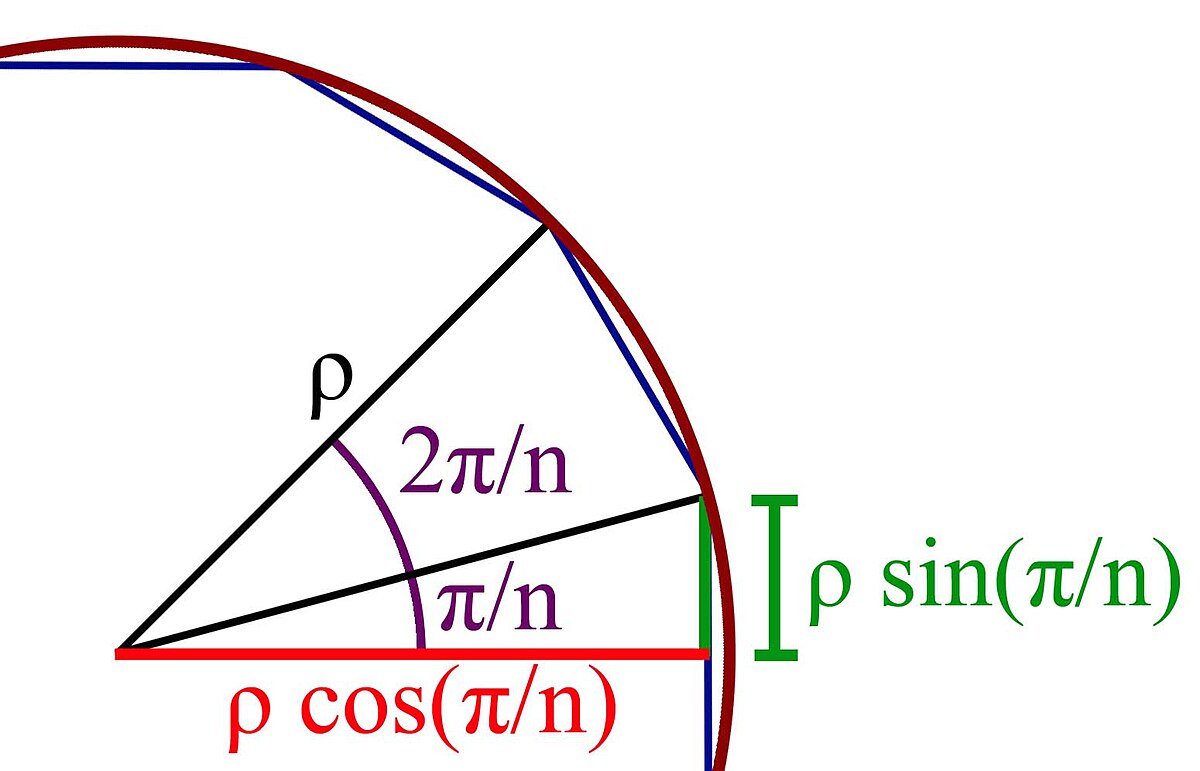
La figure explicative est sur la droite. Pour plus de simplicité, on oriente le polygone de telle manière que l'arête située la plus à droite soit verticale. L'angle associé à une arête est de mesure 2π/n. Il est néanmoins plus simple de considérer les demi-angles, la longueur d'une arête, égale à p/n s'exprime de la manière suivante :

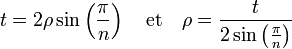
La longueur d'une arête est en effet deux fois celle du segment vert sur la figure. La surface a du polygone est la somme des aires de n triangles isocèles, ayant pour hauteur le segment en rouge sur la figure et pour base une arête. Ce qui donne la formule :

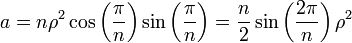
En remplaçant ρ par sa valeur, on obtient :

 

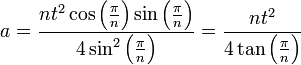
Côtés	Nom	Aire exacte si t = 1	Demi périmètre si ρ = 1
3	Triangle équilatéral		2,5980762
4	Carré		2.8284271
5	Pentagone régulier		2,9389263
6	Hexagone régulier		3,000000
7	Heptagone régulier		3,0371862
8	Octogone régulier		3,0614675
9	Ennéagone régulier		3,0781813
10	Décagone régulier		3,0901699
11	Hendécagone régulier		3,0990581
12	Dodécagone régulier		3,1058285
13	Triskaidécagone régulier		3,1111036
14	Tétradécagone régulier		3,1152931
15	Pentadécagone régulier		3,1186754
16	Hexadécagone régulier		3,1214452
17	Heptadécagone régulier		3,1237418
18	Octadécagone régulier		3,1256672
19	Ennéadécagone		3,1272972
20	Icosagone		3,1286893
100	Hectagone		3,1410759
1 000	Chiliagone		3,1415875
10 000	Myriagone		3,1415926

On remarque que, si le rayon est égal à 1, le demi-périmètre s'approche de plus en plus de π.