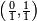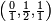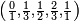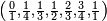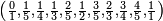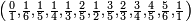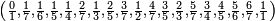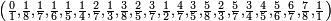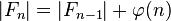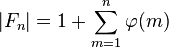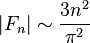Suite de Farey - Définition

Introduction

En mathématiques, la suite de Farey d'ordre n est la suite des fractions irréductibles entre 0 et 1 dont le dénominateur est inférieur ou égal à n et en ordre croissant.

Chaque suite de Farey commence avec la valeur 0, décrite par la fraction 0 / 1, et finit avec la valeur 1, décrite par la fraction 1 / 1 (bien que certains auteurs omettent ces termes).

Une suite de Farey est quelquefois appelée série de Farey, ce qui n'est pas véritablement correct, les termes n'étant pas additionnés.

Exemples

Les suites de Farey d'ordre 1 à 8 sont :

Propriétés

Nombre de termes d'une suite de Farey

La suite de Farey d'ordre n contient tous les éléments des suites de Farey d'ordre inférieur. En particulier, F_n contient tous les éléments de la suite F_{n − 1}, ainsi qu'une fraction supplémentaire pour chaque entier inférieur à n et premier avec n. Ainsi, la suite F₆ est composée des éléments de la suite F₅ auxquels il faut ajouter les fractions 1 / 6 et 5 / 6. Le terme médian d'une suite de Farey est toujours 1 / 2, lorsque n > 1.

Il est possible de relier le nombre de termes de F_n (noté | F_n | ) et celui de F_{n − 1} en utilisant l'indicatrice d'Euler  :

En utilisant le fait que | F₁ | = 2, le nombre de termes de F_n peut donc s'exprimer en fonction de n de la façon suivante :

Le comportement asymptotique de | F_n | est :

Les voisins dans une suite de Farey

Les fractions qui sont des termes voisins dans une suite de Farey ont les propriétés suivantes.

Si a / b et c / d sont voisins dans une suite de Farey, avec a / b < c / d, alors leur différence a / b − c / d est égale à 1 / bd. Comme

,

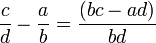
il est équivalent de dire ceci

bc − ad = 1

Ainsi 1 / 3 et 2 / 5 sont voisins dans F₅, et leur différence est 1 / 15.

L'inverse est également vrai. Si

bc − ad = 1

pour les entiers naturels a, b, c et d alors a / b et c / d sont voisins dans la suite de Farey d'ordre max(b,d).

Si a / b, p / q et c / d sont voisins dans une suite de Farey, tels que

a / b < p / q < c / d

alors p / q est le médian de a / b et c / d — c'est-à-dire que l'on a

.

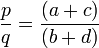
Si de plus on suppose que q > max(b,d) alors la fraction (a + c) / (b + d) est en forme irréductible.

Et, si a / b et c / d sont voisins dans une suite de Farey alors le premier terme qui apparaît entre eux lorsque l'ordre de la suite de Farey est augmenté est le médian

,

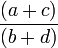
lequel apparaît en premier dans la suite de Farey d'ordre b + d.

Ainsi, le premier terme apparaissant entre 1 / 3 et 2 / 5 est 3 / 8, qui apparaît dans F₈.

L'arbre de Stern-Brocot est une structure de données montrant comment la suite est construite à partir de 0 (= 0 / 1) et 1 (= 1 / 1), en prenant les médians successifs.

Les fractions qui apparaissent comme voisines dans une suite de Farey ont des développements en fraction continue reliés. Si p / q admet le développement en fraction continue

[0;a₁,a₂,...,a_{n − 1},a_n,1]

alors les deux voisins les plus proche de p / q dans F_q ont pour développement en fraction continue

[0;a₁,a₂,...,a_{n − 1},a_n]

[0;a₁,a₂,...,a_{n − 1}]

Ainsi 3 / 8 a pour développement en fraction continue [0;2,1,1,1], et ses voisins dans F₈ sont 2 / 5 qui admet le développement [0;2,1,1] et 1 / 3 qui se développe en [0;2,1].

Cercles de Ford

Il existe une relation intéressante entre les suites de Farey et les cercles de Ford.

Pour toute fraction (réduite) p / q il existe un cercle de Ford C[p / q], qui est le cercle de rayon 1 / 2q² et de centre (p / q,1 / 2q²). Les cercles de Ford correspondant à deux fractions distinctes sont soit disjoints soit tangents - deux cercles de Ford ne peuvent pas être sécants. Si 0 < p / q < 1, alors les cercles de Ford qui sont tangents à C[p / q] sont précisément les cercles de Ford associés aux fractions qui sont voisines de p / q dans une suite de Farey.

Ainsi C[2 / 5] est tangent à C[1 / 2], C[1 / 3], C[3 / 7], C[3 / 8], etc.

Hypothèse de Riemann

Les suites de Farey sont utilisées dans deux formulations équivalentes de l'hypothèse de Riemann. Supposons que les termes de soient . Définissons , en d'autres mots d_k,n est la différence entre le k-ème terme de la n-ème suite de Farey, et le k-ème membre d'un ensemble de même nombre de points, distribués également sur l'intervalle unité. Franel et Landau ont démontré que chacun des deux énoncés  :

pour tout r>1/2, et

pour tout r>1,

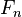
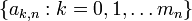
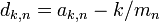
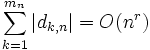
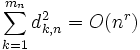
est équivalent à l'hypothèse de Riemann.